24 Section 5.3 Modeling with Polynomial Functions
a. Draw a picture of this situation.
b. Determine the length and width of the garden plot.
Show Solution
Answers
a.
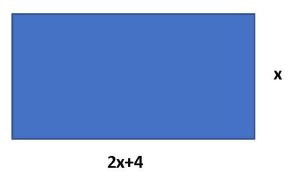
b. Area of a rectangle is calculated by [latex]A=L \times W[/latex]. With the width represented by [latex]x[/latex] and the length by [latex]2x+4[/latex], you can write the equation for area as [latex]A=x(2x+4)[/latex], then set equal to 336 and solve.
[latex]x(2x+4)=336[/latex]
[latex]2x^2+4x-336=0[/latex]
Factor out 2, then factor further.
[latex]2(x^2+2x-168)=0[/latex]
[latex]2(x+14)(x-12)=0[/latex]
This gives [latex]x=12[/latex] and [latex]x=-14[/latex]. Since the width/length cannot be negative, this means that the width of the plot is 12 ft. Then calculate the length [latex]2(12)+4[/latex], which is 28 ft.