3 Section 1.4: Linear Functions
Example 1
Using the graph below find the equation of the each of the lines below.
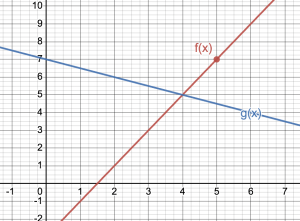
Show Solution
To find the equation for [latex]g(x)[/latex] we know that the y-intercept is 7. So, [latex]g(x) = mx+7[/latex]. Now we find the slope picking two points [latex](0,7)[/latex] and [latex](4,5)[/latex]. So, [latex]m = \frac{5-7}{4-0} = \frac{-2}{4} = \frac{-1}{2}[/latex]. Thus, [latex]g(x) = \frac{-1}{2}x+7[/latex].
To find the equation of [latex]f(x)[/latex] we will first find the slope using the points [latex](4,5)[/latex] and [latex](5,7)[/latex]. So, [latex]m = \frac{7-5}{5-4} = 2[/latex]. Writing in point slope form using the point [latex](5,7)[/latex], then [latex]f(x) = 7 + 2(x-5)[/latex].
Example 2
Rewrite the following equation in slope intercept form.
a. [latex]3(x+y) = 6[/latex]
b. [latex]\frac{x+y}{2} = 10[/latex]
Show Solution
a.
\begin{align*}
3x+3y &= 6 \\
3y &= -3x + 6 \\
y &= -x + 2
\end{align*}
b.
\begin{align*}
\frac{x+y}{2} &= 10 \\
x+y &= 20 \\
y &= -x + 20
\end{align*}
Example 3
Find an equation of the line determined by the following conditions. Write the answer in point slope form whenever possible.
- The line with slope [latex]\frac{2}{3}[/latex] and passes through the point [latex](5,4)[/latex]
- The line passing through the points [latex](2,5)[/latex] and [latex](5,6)[/latex]
- The line passing through [latex](2,3)[/latex] and is perpendicular to the line [latex]20x+5y = 4[/latex].
Show Solution
a. [latex]y = 4 + \frac{2}{3}(x-5)[/latex]
b. The slope is [latex]m = \frac{6-5}{5-2} = \frac{1}{3}[/latex]. So writing in point slope form using the point [latex](2,5)[/latex] the equation is [latex]y = 5 + \frac{1}{3}(x-2)[/latex].
c. First we need to find the slope of [latex]20x+5y = 4[/latex]. Rewriting in slope intercept form by solving for [latex]y[/latex] this is [latex]y = -4x+\frac{4}{5}[/latex]. So the equation of our line will have slope [latex]m = \frac{1}{4}[/latex]. So the equation of our line in point slope form is [latex]y = 3 + \frac{1}{4}(x-2)[/latex].
Example 4
A local bakery in Durango is looking to model the relationship between the number of cupcakes sold and the price per cupcake. Suppose 40 cupcakes were sold a day when the price was $7, but when the price when down to $4, they sold 120 cupcakes.
a. Find a formula for the linear function [latex]P[/latex], that models the price of the cupcake [latex]P = f(x)[/latex] as a function of number of cupcakes sold, [latex]x[/latex].
b. What do the slope and [latex]P[/latex]-intercept mean in the model you found in part a? Does the [latex]P[/latex]-intercept make sense in context?
c. Find [latex]f(200)[/latex] and interpret what this value means.
d. How many cupcakes would be sold if the price was [latex]$6[/latex]?
Show Solution
a. First we find the slope using the points [latex](40, 7)[/latex] and [latex](120,4)[/latex] so, m = [latex]\frac{4-7}{120-40} = \frac{-3}{80}[/latex]. Then plugging in a point [latex](50,7)[/latex] to solve for [latex]b[/latex] we get [latex]7 = \frac{-3}{80}(40) + b[/latex], so [latex]b = 8.5[/latex]. Thus, [latex]P = f(x) = \frac{-3}{80}x+8.5[/latex].
b. Slope: for each cupcake sold, the price should decrease by [latex]\frac{3}{80}[/latex] cents. [latex]P[/latex]-intercept: if the number of cupcakes sold was 0, then the price would be $8.5. The p-intercept does not make sense in context.
c. [latex]f(200) = \frac{-3}{80}(200) + 8.5 = 1[/latex]. In order to sell 200 cupcakes, the price should be $1.
d. [latex]6 = \frac{-3}{80}x + 8.5[/latex] then [latex]-2.5 = \frac{-3}{80}x[/latex] solving for [latex]x[/latex] we get [latex]x = \frac{200}{3} = 66.67[/latex]. So, about 66 cupcakes would be sold if the price was $6.