20 Section 4.4: Finding Angles
Example 1
Suppose a 30-foot ladder is leaning against a building which is 25 feet above the ground. What angle in degrees does the ladder make with the building?
Show Solution
First let us draw a picture.
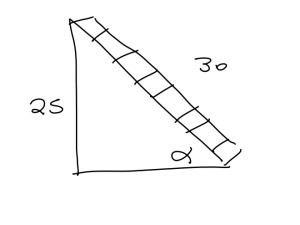
Now, we will find our angle [latex]\alpha[/latex] using the definition of the sine function. So, we have [latex]\sin(\alpha) = \frac{25}{30}[/latex]. Rewriting this statement using inverses we can say that [latex]\alpha = \arcsin(\frac{25}{30}) = 56.44^{\circ}[/latex].
Example 2
Solve each of the equations exactly on the interval [latex][0,2\pi][/latex].
a. [latex]2\sin(\beta) = 1[/latex]
b. [latex]5\tan(\beta) + 4 = 9[/latex]
c. [latex]4\cos^2(x) + 2 = 5[/latex]
d. [latex]5\sqrt{2}\sin(\alpha) - 4\sqrt{2}\sin(\alpha) + 1 = 0[/latex]
Show Solution
a. First we divide by 2 on both sides to get [latex]\sin(\beta) = \frac{1}{2}[/latex]. Then using the unit circle, we get [latex]\beta = \frac{\pi}{6}, \frac{5\pi}{6}[/latex].
b. First we subtract 4 and divide by 5 on both sids to get [latex]\tan(\beta) = 1[/latex]. Then using the unit circle, we get [latex]\beta = \frac{\pi}{4}, \frac{5\pi}{4}[/latex].
c. Isolate [latex]\cos^2(x)[/latex] first to get [latex]\cos^2(x) = \frac{3}{4}[/latex]. Then take the square root of both sides to get [latex]\cos(x) = \pm \sqrt{\frac{3}{4}} = \frac{\sqrt{3}}{2}[/latex]. Then using the unit circle, we get [latex]x = \frac{\pi}{6}, \frac{5\pi}{6}, \frac{7\pi}{6}, \frac{11\pi}{6}[/latex].
d. First combine like terms to get [latex]\sqrt{2}\sin(\alpha) + 1 = 0[/latex]. Then subtract 1 on both sides and divide by [latex]\sqrt{2}[/latex] to get [latex]\sin(\alpha) = \frac{-1}{\sqrt{2}}[/latex]. Then using the unit circle, we get [latex]\alpha = \frac{3\pi}{4}, \frac{5\pi}{4}[/latex].
Example 3
Solve each of the following equations exactly and approximately on the interval [latex][0,2\pi][/latex]
a. [latex]\sin(x) = 0.7[/latex]
b. [latex]2\cos(x) = 1-\cos(x)[/latex]
c. [latex]6\sin(x) + 5 = 4[/latex]
d. [latex]5\tan(x) = 3[/latex]
Show Solution
a. We first use inverse sine to find the first solution to get [latex]x = \arcsin(0.7) \approx 0.775[/latex] radians. Then, we can use symmetry of the unit circle to get the second answer [latex]x = \pi - \arcsin(0.7) \approx 2.366[/latex] radians.
b. First we combine like terms to get [latex]3\cos(x) = 1[/latex] then divide by 3 on both sides to get [latex]\cos(x) = \frac{1}{3}[/latex]. Then we use inverse cosine to find the first solution to get [latex]x = \arccos(\frac{1}{3}) \approx 1.23[/latex] radians. Then, we can use symmetry of the unit circle to get our second answer [latex]x = 2\pi - \arccos(\frac{1}{3}) = 5.052[/latex] radians.
c. First we isolate the sine function on one side to get [latex]\sin(x) = \frac{-1}{6}[/latex]. We use inverse sine to get [latex]x = \arcsin(\frac{-1}{6})[/latex]. This angle is not in our interval of [latex][0,2\pi][/latex]. So, we can add [latex]2\pi[/latex] to get an angle in our correct interval to get [latex]x = 2\pi + \arcsin(\frac{-1}{6}) \approx 6.116[/latex] radians. Our second answer will come from symmetry of the unit circle [latex]x = \pi - \arcsin(\frac{-1}{6})[/latex].
d. Isolate [latex]\tan(x)[/latex] on one side to get [latex]\tan(x) = \frac{3}{5}[/latex]. Then using inverse trig we find our first solution [latex]x = \arctan(\frac{3}{5}) \approx 0.540[/latex] radians. Then using symmetry of the unit circle we find our second answer of [latex]x = \pi + \arctan(\frac{3}{5}) \approx 3.682[/latex] radians.
Example 4
Suppose we have a right triangle with side lengths 3 and 8. Determine all missing sides and angles in the right triangle. Give your answer in radians.
Show Solution
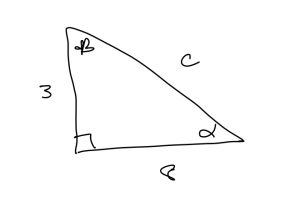
We can find the missing side using the pythagorean theorem. So, [latex]c^2 = 3^2 + 8^2 = 73[/latex], so [latex]c = \sqrt{73}[/latex]. Then we can find the missing angles by using tangent. So, [latex]\tan(\alpha) = \frac{3}{8}[/latex]. Rewriting this using inverses: [latex]\alpha = \arctan(\frac{3}{8}) \approx 0.358[/latex] radians. Similarly, we know that [latex]\tan(\beta) = \frac{8}{3}[/latex]. Rewriting this using inverses: [latex]\beta = \arctan(\frac{8}{3}) \approx 1.21[/latex] radians.