18 Section 4.2: The Tangent Function
Example 1
Find the exact values below.
a. [latex]\tan(\frac{-\pi}{6})[/latex]
b. [latex]\tan(\frac{-2\pi}{3})[/latex]
c. [latex]\tan(7\pi)[/latex]
d. [latex]\tan(\frac{13\pi}{4})[/latex]
Show Solution
a. [latex]\tan(\frac{-\pi}{6}) = \frac{-1}{\sqrt{3}}[/latex]
b. [latex]\tan(\frac{-2\pi}{3}) = \sqrt{3}[/latex]
c. [latex]\tan(7\pi) = 0[/latex]
d. [latex]\tan(\frac{13\pi}{4}) = 1[/latex]
Example 2
Suppose we have a right triangle with angle [latex]\beta= 53^{\circ}[/latex] and side opposite [latex]\beta[/latex] of length 9. Find all missing sides and angles.
Show Solution
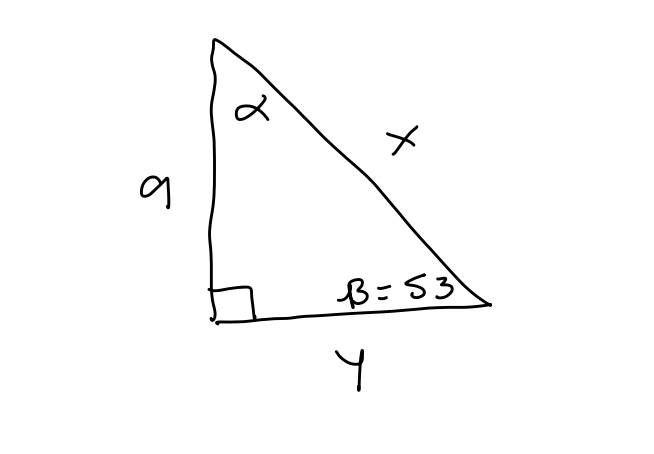

First we will find the missing angle [latex]\alpha[/latex]. since the angles of a right triangle add up to 180 then [latex]\alpha = 37^\circ[/latex]. Next, we will use the definition of sine to solve for x. So, [latex]\sin(53^{\circ}) = \frac{9}{x}[/latex]. Solving for [latex]x[/latex] we get , [latex]x = \frac{9}{\sin(53^{\circ})} \approx 11.27[/latex]. Now, we will use tangent to solve for [latex]y[/latex]. So, [latex]tan(53^\circ) = \frac{9}{y}[/latex]. Isolating [latex]y[/latex], we get [latex]y = \frac{9}{\tan(53^{\circ})} \approx 6.78[/latex].
Example 3
Suppose you are making an angle of 7 degrees with the clocktower at Fort Lewis College. You are standing 2600 feet away from the building. How tall is the clocktower? Round to two decimal places.
Show Solution
First we will draw a picture.

To find the height of the clocktower, [latex]x[/latex], we will use tangent. Thus, [latex]\tan(7^\circ) = \frac{x}{2600}[/latex]. Solving for [latex]x[/latex] we get [latex]x = 2600\tan(7) \approx 319.24[/latex] feet.