17 Section 4.1: Right Triangles
Example 1
Use the triangle below to evaluate the following. Make sure your answers are in reduced fractions.
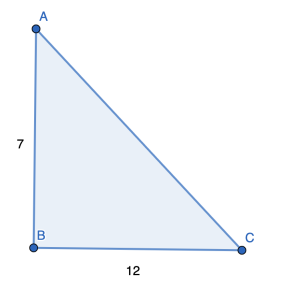
a. [latex]\sin(A)[/latex]
b. [latex]\cos(A)[/latex]
c. [latex]\cos(C)[/latex]
d. [latex]\sin(C)[/latex]
Show Solution
First, we will find the hypotenuse 'c' using the pythagorean theorem. Since, [latex]12^2+7^2 = c^2[/latex] which gives [latex]c^2 = 193[/latex], so [latex]c = \sqrt{193}[/latex]. Then,
a. [latex]\sin(A) = \frac{opp}{hyp} = \frac{12}{\sqrt{193}}[/latex]
b.[latex]\cos(A) = \frac{adj}{hyp} = \frac{7}{\sqrt{193}}[/latex]
c. [latex]\cos(C) = \frac{adj}{hyp} = \frac{12}{\sqrt{193}}[/latex]
d. [latex]\sin(C) = \frac{opp}{hyp} = \frac{7}{\sqrt{193}}[/latex]
Example 2
For each of the following scenarios determine all missing angles and sides. Simplify if possible.
a. A right triangle with one non-right angle of measure [latex]23^\circ[/latex] and hypotenuse length [latex]12[/latex]
b. A right triangle with one non-right angle of measure [latex]72^\circ[/latex] and side length opposite that angle length [latex]6[/latex].
Show Solution
a. Let us first draw a triangle and label the sides.
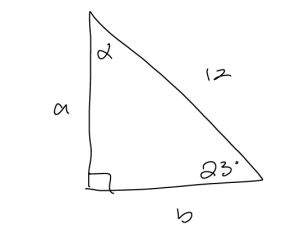
First we will solve for the missing angle [latex]\alpha[/latex]. Since the interior angles of a triangle must add up to [latex]180^\circ[/latex] and the right angle has a measure a measure of [latex]90^\circ[/latex], then [latex]\alpha + 23 = 90[/latex]. Solving for [latex]\alpha = 67^{\circ}[/latex].
Now we solve for side a by using the definition of sine. So, [latex]\sin(23^\circ) = \frac{opp}{hyp} = \frac{a}{12}[/latex]. Then we multiply on 12 to both sides to get [latex]a = 12\sin(23^\circ) \approx = 4.68[/latex].
Next we solve for side b by using the definition of cosine. So, [latex]\cos(23^\circ) = \frac{adj}{hyp} = \frac{a}{12}[/latex]. Then we multiply on 12 to both sides to get [latex]b = 12\cos(23^\circ) \approx = 11.05[/latex].
b. Let us first draw a triangle and label the sides.
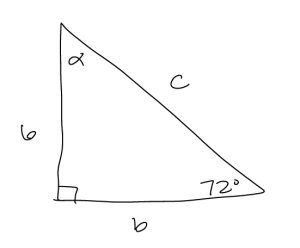
First we will solve for the missing angle [latex]\alpha[/latex]. Since the interior angles of a triangle must add up to [latex]180^\circ[/latex] and the right angle has a measure a measure of [latex]90^\circ[/latex], then [latex]\alpha + 72 = 90[/latex]. Solving for [latex]\alpha = 18^{\circ}[/latex].
Now we solve for the hypotenuse by using the definition of sine. So, [latex]\sin(72^\circ) = \frac{opp}{hyp} = \frac{6}{c}[/latex]. Then we multiply on c on both sides to get [latex]c \cdot \sin(72^\circ) = 6[/latex]. Then divide by [latex]\sin(72^\circ)[/latex] on both sides to get [latex]c = \frac{6}{\sin(72^\circ)} \approx 6.308[/latex].
Next we will solve for side b. Using the definition of cosine we have [latex]\cos(72^\circ) = \frac{adj}{hyp} = \frac{\frac{6}{\sin(72^\circ)}}{b}[/latex]. Then we multiply by b on both sides to get [latex]b \cdot \cos(72^\circ) = \frac{6}{\sin(72^\circ)}[/latex]. Then dividing both sides by [latex]\cos(72^\circ)[/latex] we get [latex]b= \frac{\frac{6}{\sin(72^\circ)}}{\cos(72^\circ)} = \frac{6\cos(62^\circ)}{\sin(72^\circ)} \approx 1.95[/latex].
Example 3
Show Solution
Let us first draw a picture.
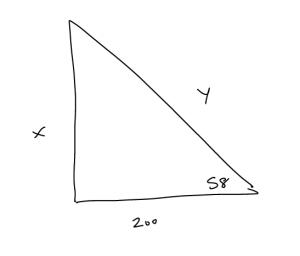
We want to solve for tall the building is which is length 'x'. First, we determine the length of the hypotenuse y using cosine. So, [latex]\cos(58^\circ) = \frac{200}{y}[/latex]. Solving for y we get [latex]y = \frac{200}{\cos(58^\circ)}[/latex]. So, then we solve for x by using sine. Thus, [latex]\sin(58^\circ) = \frac{x}{\frac{200}{\cos(58^\circ)}}[/latex]. Isolating x we get [latex]x = \frac{200}{\cos(58^\circ)} \cdot \sin(58^\circ) = \frac{200\sin(58^\circ)}{\cos(58^\circ)} \approx[/latex] 320.07 feet. So, the building is approximately 320.06 feet tall.