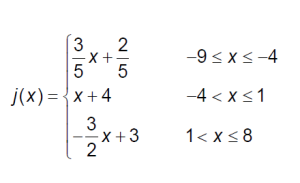8 Section 1.9 Combining Functions
a. Determine the exact value of [latex](f+g)(1)[/latex].
b. Determine the exact value of [latex](g-f)(0)[/latex].
c. Determine the exact value of [latex](f \cdot g)(2)[/latex].
d. Are there any values of [latex]x[/latex] for which [latex]\left(\frac{f}{g}\right)(x)[/latex] is undefined? If not, explain why. If so, determine the value(s) and justify your answer.
Show Solution
Answers
a. [latex](f+g)(1)=f(1)+g(1)[/latex]. Substitute 1 into both equations. [latex]f(1)=-1[/latex] and [latex]g(1)=15[/latex]. Finally, [latex](f+g)(1)=-1+15=14[/latex].
b. [latex](g-f)(0)=g(0)-f(0)[/latex]. After substituting 0 into both equations, [latex]g(0)=19[/latex] and [latex]f(0)=0[/latex]. Finally, [latex](g-f)(0)=19-0=19[/latex].
c. [latex](f \cdot g)(2)=f(2)\cdot g(2)[/latex]. Then substitute 2 into both equations; [latex]f(2)=4[/latex] and [latex]g(2)=11[/latex]. Then [latex](f \cdot g)(2)=4\cdot 11=44[/latex].
d. [latex]\left(\frac{f}{g}\right)(x)=\frac{f(x)}{g(x)}[/latex]. This makes [latex]\left(\frac{f}{g}\right)(x)=\frac{x^3-2x}{19-4x}[/latex]. This fraction would be undefined when the denominator is 0, so we need to solve [latex]19-4x=0[/latex]. [latex]x=\frac{19}{4}[/latex], so it would be at this value that would make [latex]\left(\frac{f}{g}\right)(x)[/latex] undefined.
2. Let the graph below represent [latex]j(x)[/latex].
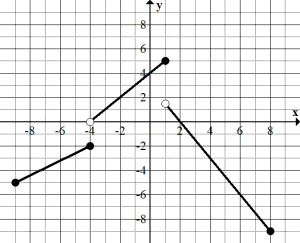
Write the piecewise equation that represents [latex]j(x)[/latex].
Show Solution
Answers
Notice that the graph has three pieces, so you will need to write three separate equations, then bring them together into the proper piecewise function notation. Also notice that all three pieces are linear.
First part: This graph clearly passes through [latex](-9,-5)[/latex] and [latex](-4,-2)[/latex]. Then find the slope, [latex]m=\frac{3}{5}[/latex]. Then determine the vertical intercept.
[latex]-5=\frac{3}{5}(-9)+b[/latex]
[latex]b=\frac{2}{5}[/latex]
First equation is [latex]y=\frac{3}{5}x+\frac{2}{5}[/latex].
Section part: This graph clearly passes through [latex](-4,0)[/latex] and [latex](0,4)[/latex]. (Do not worry that there is an open circle on [latex](-4,0)[/latex] for the purposes of creating the line.) The slope here is [latex]m=1[/latex]. Notice that the vertical intercept is clearly marked, [latex](0,4)[/latex], so you can write the equation for this piece.
Second equation is [latex]y=x+4[/latex].
Third part: This pieces clearly passes through [latex](2,0)[/latex] and [latex](6,-6)[/latex]. This means that the slope is [latex]m=-\frac{3}{2}[/latex]. Then we determine the vertical intercept.
[latex]0=-\frac{3}{2}(2)+b[/latex]
[latex]b=3[/latex]
Third equation is [latex]y=-\frac{3}{2}x+3[/latex].
Now, this needs to be written into proper notation with the domains that go with each piece.