6 Section 1.7 Inverse Functions
a. [latex]f(x)=2(x-3)^3+4[/latex]
b. [latex]g(x)=\frac{3}{x-7}[/latex]
Show Solution
Answers
a. Start by writing this as [latex]y=2(x-3)^3+4[/latex], then solve for [latex]x[/latex].
[latex]y=2(x-3)^3+4[/latex]
[latex]y-4=2(x-3)^3[/latex]
[latex]\frac{y-4}{2}=(x-3)^3[/latex]
[latex]\sqrt[3]{\frac{y-4}{2}}=x-3[/latex]
[latex]\sqrt[3]{\frac{y-4}{2}}+3=x[/latex]
[latex]x=f^{-1}(y)=\sqrt[3]{\frac{y-4}{2}}+3[/latex]
b. Write as [latex]y=\frac{3}{x-7}[/latex], then solve for [latex]x[/latex].
[latex]y=\frac{3}{x-7}[/latex]
[latex]y \times (x-7)=3[/latex]
[latex]x-7=\frac{3}{y}[/latex]
[latex]x=g^{-1}(y)=\frac{3}{y}+7[/latex]
2. Use the graph of [latex]f(x)[/latex] to answer the questions below.
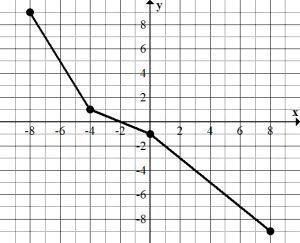
a. [latex]f^{-1}(-4)[/latex]
b. [latex]f^{-1}(5)[/latex]
c. [latex]f^{-1}(0)[/latex]
Show Solution
Answers
When finding inverse values from the original function, recall that the variables have switched roles.
a. To find [latex]f^{-1}(-4)[/latex], look at the graph where [latex]y=-4[/latex]. The corresponding [latex]x[/latex] value is 3. Thus, [latex]f^{-1}(-4)=3[/latex].
b. To find [latex]f^{-1}(5)[/latex], look at the graph where [latex]y=5[/latex]. The corresponding [latex]x[/latex] value is -6. So, [latex]f^{-1}(5)=-6[/latex]
c. [latex]f^{-1}(0)[/latex], look at the graph where [latex]y=0[/latex]. The corresponding [latex]x[/latex] value is -2. Thus, [latex]f^{-1}(0)=-2[/latex].