5 Section 1.6 Composite Functions
a. Find and simplify [latex]f(1-x)[/latex].
b. Find and simplify [latex]f(g(x))[/latex].
c. Find and simplify [latex]g(f(x))[/latex].
Show Solution
Answers
a.
[latex]f(1-x)=(1-x)^2+3[/latex]
[latex]f(1-x)=(1-x)(1-x)+3[/latex]
[latex]f(1-x)=x^2-2x+4[/latex]
b.
[latex]f(g(x))=f(\frac{2}{x})[/latex]
[latex]f(g(x))=(\frac{2}{x})^2+3[/latex]
[latex]f(g(x))=\frac{4}{x^2}+3[/latex]
c.
[latex]g(f(x))=\frac{2}{x^2+3}[/latex]
2. For each function below, find two simpler functions [latex]f[/latex] and [latex]g[/latex] so that the given functions can be written as [latex]f(g(x))[/latex].
Note: you cannot use [latex]g(x)=x[/latex].
a. [latex]h(x)=\frac{3}{\sqrt{x+1}}[/latex]
b. [latex]j(x)=\sqrt[3]{\frac{2x}{7}}[/latex]
c. [latex]k(x)=(x^2-3)^4+1[/latex]
Show Solution
Answers
a. One option: [latex]f(x)=\frac{3}{x}[/latex] and [latex]g(x)=\sqrt{x+1}[/latex]. Another option: [latex]f(x)=\frac{3}{\sqrt{x}}[/latex] and [latex]g(x)=x+1[/latex].
b. One option: [latex]f(x)=\sqrt[3]{x}[/latex] and [latex]g(x)=\frac{2x}{7}[/latex]. Another option: [latex]f(x)=\sqrt[3]{\frac{x}{7}}[/latex] and [latex]g(x)=2x[/latex].
c. One option: [latex]f(x)=x^4+1[/latex] and [latex]g(x)=x^2-3[/latex]. Another option: [latex]f(x)=x+1[/latex] and [latex]g(x)=(x^2-3)^4[/latex].
3. An oil spill is spreading in a roughly circular shape. The radius, [latex]r[/latex], is growing by 10 feet per hour.
a. Construct a function [latex]r[/latex] that represents the radius [latex]r[/latex] as a function of time [latex]t[/latex], in hours since the oil spill.
b. The area [latex]A[/latex] of the spill is a function of the radius [latex]r[/latex], given by [latex]A(r)=\pi r^2[/latex]. Determine a formula such that [latex]A \circ r[/latex].
c. Explain the meaning of the formula you found in part a.
Show Solution
Answers
a. [latex]r(t)=10t[/latex]
b. [latex]A(t)=\pi(10t)^2=100\pi t^2[/latex]
c. The formula gives the area of the oil spill, ft2, in terms of [latex]t[/latex], time in hours.
4. Use the given graphs to compute the following quantities, if possible.
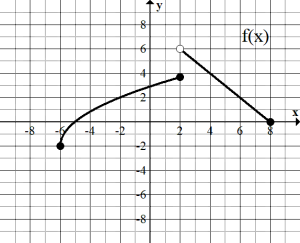
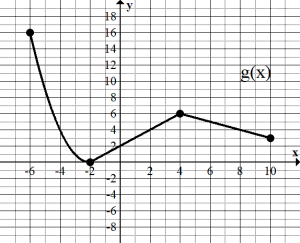
a. [latex]f(g(4))[/latex]
b. [latex]f(g(-4))[/latex]
c. [latex]g(f(-6))[/latex]
d. [latex]g(f(6))[/latex]
Show Solution
Answers
a. First, find [latex]g(4)[/latex] which is 6. Then compute[latex]f(6)[/latex] which is 2. So [latex]f(g(4))=2[/latex].
b. First, find [latex]g(-4)[/latex] which is 4. Then compute [latex]f(4)[/latex] which is 4. So [latex]f(g(-4))=4[/latex].
c. First, find [latex]f(-6)[/latex] which is -2. Then compute [latex]g(-2)[/latex] which is 0. So [latex]g(f(-6))=0[/latex].
d. First, find [latex]f(6)[/latex] which is 2. Then computer [latex]g(2)[/latex] which is 4. So [latex]g(f(6))=4[/latex].