4 Section 1.5: Quadratic Functions
Example 1
Find an equation of a parabola given the graph below.
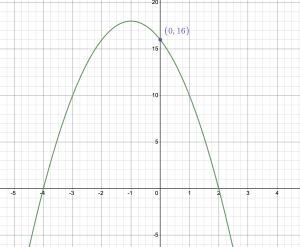
Show Solution
a. The x-intercepts are at [latex](2,0)[/latex] and [latex](-4,0)[/latex]. So, plugging this into factored form we get [latex]f(x) = a(x-2)(x+4)[/latex]. Then we plug in [latex](0,16)[/latex] to solve for [latex]a[/latex]. So [latex]16 = a(0-2)(0+4)[/latex]. So, [latex]a = -2[/latex]. Thus, [latex]f(x) = -2(x-2)(x+4)[/latex]
Example 2
Find a formula for a quadratic function given the following properties
- [latex]y[/latex]-intercept of 6 and vertex of [latex](1,-1)[/latex]
- [latex]y[/latex]-intercept of -3 and x-intercepts of 2 and -3
- vertex of [latex](-4,3)[/latex] and passes through the point [latex](2,5)[/latex]
Show Solution
a. Plugging the vertex into vertex form, we have [latex]y = a(x-1)^2-1[/latex]. Then we plug in the y-intercept [latex](0,6)[/latex] to solve for [latex]a[/latex], so [latex]6 = a(0-1)^2-1[/latex]. Solving for a we get [latex]a = 7[/latex]. Thus, [latex]y = 7(x-1)^2-1[/latex].
b. Plugging the vertex into factored form we have [latex]y = a(x-2)(x+3)[/latex]. Then we plug in the [latex]y[/latex]-intercept [latex](0,-3)[/latex] to solve for a so [latex]-3 = a(0-2)(0+3)[/latex]. Solving for [latex]a[/latex] we get [latex]a = \frac{1}{2}[/latex]. Thus, [latex]y = \frac{1}{2}(x-2)(x+3)[/latex].
c. Plugging the vertex into vertex form we have [latex]y = a(x+4)^2+3[/latex]. Then we plug in the point [latex](2,5)[/latex] to solve for [latex]a[/latex] so [latex]5 = a(2+4)^2 + 3[/latex]. Solving for [latex]a[/latex] we get [latex]a = \frac{1}{18}[/latex]. Thus, [latex]y = \frac{1}{18}(x+4)^2+3[/latex].
Example 3
Find the vertex, x-intercepts, and y-intercept of each of the following quadratics
a. [latex]y = x^2-3x-18[/latex]
b. [latex]y = 4x^2-4x-8[/latex]
c. [latex]y = x^2+3x-21[/latex]
d. [latex]y = 2(x-7)^2+1[/latex]
Show Solution
a. [latex]y = x^2-3x-18[/latex].
Vertex: [latex](1.5, -20.25)[/latex]
x-intercepts: [latex](6,0)[/latex] and [latex](-3,0)[/latex]
y-intercept: [latex](0,-18)[/latex]
b. [latex]y = 4x^2-4x-8[/latex]
Vertex: [latex](0.5,-9)[/latex]
x-intercepts: [latex](-1,0)[/latex] and [latex](2,0)[/latex]
y-intercept: [latex](0,-8)[/latex]
c. [latex]y = x^2+3x-21[/latex]
Vertex: [latex](-1.5, -23.25)[/latex]
x-intercepts: [latex](\frac{-3+\sqrt{93}}{2}, 0), (\frac{-3-\sqrt{93}}{2}, 0)[/latex]
y-intercept: [latex](0,-21)[/latex]
d. [latex]y = 2(x-7)^2+1[/latex]
Vertex: [latex](7, 1)[/latex]
x-intercepts: none
y-intercepts: [latex](0,99)[/latex]
Example 4
A ball is thrown in the air. Its height in meters as a function of time, in seconds, is given by [latex]h(t) = -4.9t^2+14.7t+19.6[/latex].
a. Determine the maximum height of the ball.
b. Determine the time that the ball hits the ground.
Show Solution
a. The maximum height of the ball is 30.625 meters.
b. The ball hits the ground at [latex]t = 4[/latex] seconds.