2 Section 1.2: Functions: Modeling Relationships
Example 1
A model rocket is launched in the air the height of the rocket, in feet, as a function of time in seconds is given by the formula [latex]h(t) = -16t^2-200t+336[/latex]. Determine a reasonable domain and range for this model. Hint: Use Desmos to graph the function.
Show Solution
Reasonable domain: [latex][0,2][/latex]
Reasonable range: [latex][0,336][/latex]
Example 2
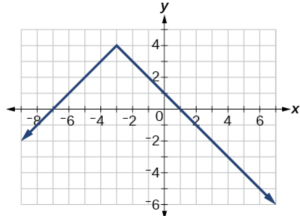
For the graph of [latex]f(x)[/latex] below determine the following:
a. [latex]f(4)[/latex]
b. Solve where [latex]f(x) = 1[/latex]
c. Domain
d. Range
Show Solution
a. [latex]f(4) = -3[/latex]
b. [latex]x = 0, -6[/latex]
c. Domain: [latex](-\infty, \infty)[/latex]
d. Range: [latex](-\infty, 4][/latex]
Example 3
For the function [latex]f(x) = 8x^2 -7x +3[/latex]:
a. Evaluate [latex]f(-2)[/latex]
b. Evaluate [latex]f(3)[/latex]
c. Solve [latex]f(x) = 4[/latex]
d. Find [latex]f(h)[/latex]
e. Find [latex]f(x+h)[/latex]
Show Solution
a. [latex]f(-2) = 49[/latex]
b. [latex]f(3) = 54[/latex]
c. [latex]x = \frac{-1}{8}[/latex] and [latex]x = 1[/latex]
d. [latex]f(h) = 8h^2-7h+3[/latex]
e. [latex]f(x+h) = 8(x+h)^2 - 7(x+h) + 3 = 8(x^2+2xh+h^2) - 7x-7h + 3 = 8x^2+16xh+h^2-7x-7h+3[/latex]
Example 4
Find the domain of each of the following functions below:
a. [latex]f(x) = \frac{x-2}{x+5}[/latex]
b. [latex]g(x) = \frac{x^2+1}{x^2-2x-15}[/latex]
c. [latex]h(x) = \sqrt{-x+6}[/latex]
Show Solution
a. Domain: [latex](-\infty, -5) \cup (-5, \infty)[/latex]
b. Domain: [latex](-\infty, -3) \cup (-3,5) \cup (5, \infty)[/latex]
c. Domain: [latex](-\infty, 6][/latex]
Example 5
The table below represents the amount of money made per week after working h hours.
| h | 6 | 12.5 | 13 | 16 | 4 | 60 | 70 |
| P | 90 | 180 | 180 | 240 | 60 | 900 | 1050 |
a. Is [latex]P[/latex] a function of [latex]h[/latex]?
b. Let [latex]P = f(h)[/latex] denote the amount of made made after [latex]h[/latex] hours. Evaluate and interpret [latex]f(60)[/latex].
c. Solve [latex]f(t) = 180[/latex].
d. Interpret your results from part c.
Show Solution
a. Yes
b. [latex]f(60) = 900[/latex]. If a person works 60 hours a week they will make $900.
c. t = 12.5 and t = 13.
d. If a person works 12.5 hours or 13 hours they will make $180.