14 Section 3.2: Modeling with Exponential Functions
Example 1
For each of the following functions determine
- y-intercept
- horizontal asymptote
- range
- sketch of the graph
a. [latex]f(x) = 3(1.2)^x+5[/latex]
b. [latex]g(x) = 15(0.8)^x-6[/latex]
c. [latex]h(x) = -2(\frac{6}{5})^x[/latex]
d. [latex]j(x) = -(\frac{3}{4})^x + 3[/latex]
Show Solution
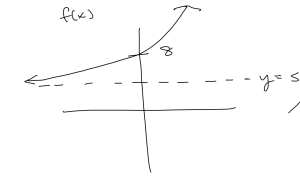
a. [latex]f(x) = 3(1.2)^x+5[/latex]
- y-intercept: [latex]f(0) = 3(1.2)^0+5 = 3+5 = 8[/latex]
- horizontal asymptote: [latex]y = 5[/latex]
- range: [latex](5, \infty)[/latex]
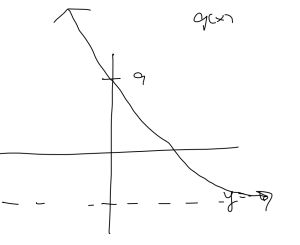
b. [latex]g(x) = 15(0.8)^x-6[/latex]
- y-intercept: [latex]g(0) = 15(0.8)^0-6 = 15-6 = 9[/latex]
- horizontal asymptote: [latex]y = -6[/latex]
- range: [latex](-6, \infty)[/latex]
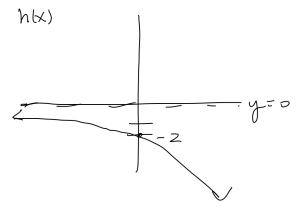
c. [latex]h(x) = -2(\frac{6}{5})^x[/latex]
- y-intercept: [latex]h(0) = -2(\frac{6}{5})^0 = -2[/latex]
- horizontal asymptote: [latex]y = 0[/latex]
- range: [latex](-\infty, 0)[/latex]
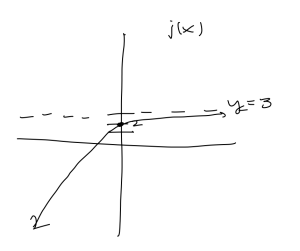
d. [latex]j(x) = -(\frac{3}{4})^x + 3[/latex]
- y-intercept: [latex]j(0) = -(\frac{3}{4})^0+3 = -1+3 = 2[/latex]
- horizontal asymptote: [latex]y = 3[/latex]
- range: [latex](-\infty, 3)[/latex]
Example 2
Let [latex]f(x) = (\frac{1}{2})^x[/latex] be our parent function.
a. Write a transformed function g(x) that is a vertical shift up 6, reflection across x, and a horizontal shift right 2 of the function f(x).
b. What is the long term behavior of the function?
c. What is the y-intercept?
Show Solution
a. [latex]g(x) = -(1/2)^{x-2}+6[/latex]
b. as [latex]x \rightarrow \infty, g(x) \rightarrow 6[/latex].
c. [latex]g(0) = -(\frac{1}{2})^{0-2}+6 = -(\frac{1}{2})^{-2} +6 = -4 + 6 = 2[/latex]