5.4 Rational Functions
Determine the domain of each of the following functions. In each case, write a sentence to accurately describe the domain.
a. [latex]f(x)=\frac{x^2-1}{x^2+1}[/latex]
b. [latex]g(x)=\frac{x^2-1}{x^2+3x-4}[/latex]
c. [latex]h(x)=\frac{1}{x}+\frac{1}{x-1}+\frac{1}{x-2}[/latex]
d. [latex]j(x)=\frac{(x+5)(x-3)(x+1)(x-4)}{(x+1)(x+3)(x-5)}[/latex]
e. [latex]k(x)=\frac{2x^2+7}{3x^3-12x}[/latex]
f. [latex]m(x)=\frac{5x^2-45}{7(x-2)(x-3)^2(x^2+9)(x+1)}[/latex]
Show Solution
NOTE: to find the domain of rational functions, you’ll want to determine if, and for what values, the denominator is equal to 0.
a. If we try to solve[latex]x^2+1=0[/latex], we find that there are no [latex]x[/latex] that make this denominator zero. This means that the domain of [latex]f(x)[/latex] is all real numbers.
Domain: [latex](-\infty,\infty)[/latex].
b. First,
[latex]x^2+3x-4=0[/latex]
[latex](x-1)(x+4)=0[/latex]
[latex]x=1, -4[/latex]
So the domain of this function is all real numbers except -4 and 1.
Domain: [latex](-\infty,-4)\bigcup (-4,1)\bigcup (1,\infty)[/latex].
c. Since there are three fractions, you’ll need to find what [latex]x[/latex] values make each denominator equal to 0.
For term [latex]\frac{1}{x}[/latex], this is [latex]x=0[/latex].
For term [latex]\frac{1}{x-1}[/latex], this is [latex]x=1[/latex].
For term [latex]\frac{1}{x-2}[/latex], this is [latex]x=2[/latex].
This means that the domain of [latex]h(x)[/latex] is all real numbers except 0, 1, and 2.
Domain: [latex](-\infty,0)\bigcup (0,1) \bigcup (1,2) \bigcup (2,\infty)[/latex].
d. Since the denominator is nicely factored, set each factor equal to 0. And find that [latex]x=-3,-1, 5[/latex]. The domain is all real numbers except -3, -1 and 5.
Domain: [latex](-\infty, -3)\bigcup (-3,-1)\bigcup (-1,5) \bigcup (5,\infty)[/latex].
e.
[latex]3x^3-12x=0[/latex]
[latex]3x(x^2-4)=0[/latex]
[latex]3x=0[/latex] and [latex](x-2)(x+2)=0[/latex]
[latex]x=0, -2, 2[/latex]
So the domain of [latex]k(x)[/latex] is all real numbers except -2, 0 and 2.
Domain: [latex](-\infty,-2)\bigcup (-2,0)\bigcup (0,2)\bigcup (2,\infty)[/latex].
f.
[latex]7(x-2)(x-3)^2(x^2+9)(x+1)=0[/latex]
From this, we can ignore the 7 as well as the factor [latex]x^2+9[/latex], because neither of them will equal 0. Then,
[latex]x-2=0[/latex] and [latex](x-3)^2=0[/latex] and [latex]x+1=0[/latex]
[latex]x=2, -1, 3[/latex], where 3 has multiplicity two.
The domain of [latex]m(x)[/latex] is all real numbers except -1, 2, and 3.
Domain: [latex](-\infty,-1)\bigcup (-1,2)\bigcup (2,3)\bigcup (3,\infty)[/latex]
Suppose that we want to build an open rectangular box (that is, without a top) that holds 15 cubic feet of volume. If we want one side of the base to be twice as long as the other, how does the amount of material required depend on the shorter side of the base? We investigate this question through the following sequence of prompts.
a. Draw a labeled picture of the box. Let [latex]x[/latex] represent the shorter side of the base and [latex]h[/latex] the height of the box. What is the length of the longer side of the base in terms of [latex]x[/latex]?
b. Use the given volume constraint to write an equation that relates [latex]x[/latex] and [latex]h[/latex], and solve the equation for h in terms of [latex]x[/latex].
c. Determine a formula for the surface area, [latex]S[/latex], of the box in terms of [latex]x[/latex] and [latex]h[/latex].
d. Using the constraint equation from (b) together with your work in (c), write surface area, [latex]S[/latex], as a function of the single variable [latex]x[/latex].
e. What type of function is [latex]S[/latex]? What is its domain?
f. Plot the function [latex]S[/latex] using Desmos. What appears to be the least amount of material that can be used to construct the desired box that holds 15 cubic feet of volume?
Show Solution
a. The longer side of the base will be [latex]2x[/latex].
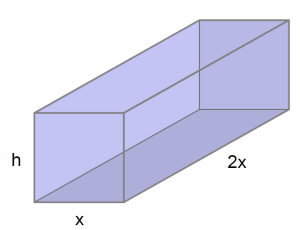b. The volume equation starts as [latex]V=x\cdot 2x\cdot h[/latex]. Substitute [latex]V=15[/latex], then solve for [latex]h[/latex].
[latex]15=x\cdot 2x\cdot h[/latex]
[latex]h=\frac{15}{2x^2}[/latex].
c. The area of a rectangular box is [latex]A=2l\cdot w+2w\cdot h+2l\cdot h[/latex]. For this box, the area is
[latex]A=2x\cdot h+2x\cdot 2x+2h\cdot 2x[/latex]
d. Using part c, substitute [latex]h=\frac{15}{2x^2}[/latex].
[latex]A=2x(\frac{15}{2x^2})+4x^2+4x(\frac{15}{2x^2}[/latex])
Simplify.
[latex]A=\frac{15}{x}+4x^2+\frac{30}(x}[/latex]
e. This is a rational function with a domain of [latex](0,\infty)[/latex].
f. DESMOS here
5.4 Exercise 9
For each rational function below, determine the function’s domain as well as the exact value of any horizontal asymptote.
a. [latex]f(x)=\frac{17x^2+34}{19x^2-76}[/latex]
b. [latex]g(x)=\frac{29}{53}+\frac{1}{x-2}[/latex]
c. [latex]h(x)=\frac{4-31x}{11x-7}[/latex]
d. [latex]r(x)=\frac{151(x-4)(x+5)^2(x-2)}{537(x+5)(x+1)(x^2+1)(x-15)}[/latex]
Show Solution
NOTE: Recall that a function is undefined if the denominator is 0, so to find the domain, start by finding when the denominator equals 0. This will give any [latex]x[/latex] values that will not be in the domain.
a.
[latex]19x^2-76=0[/latex]
[latex]x=\pm \sqrt\frac{76}{19}=\pm 2[/latex]
So this tells us that -2 and +2 are not in the domain of this function. There are no other numbers that will make the denominator equal 0, so we write the domain to exclude just -2 and +2.
Domain: [latex](-\infty, -2)\bigcup(-2,2)\bigcup(2,+\infty)[/latex]
To find the horizontal asymptote, identify the leading term (and degree) of the numerator and denominator.
Numerator: [latex]17x^2[/latex] and Denominator: [latex]19x^2[/latex]
Since these have the same degree, look at each term’s coefficient. This leads to a horizontal asymptote of [latex]y=\frac{17}{19}[/latex].
b. For purposes of domain, you can ignore [latex]\frac{29}{53}[/latex], and focus on [latex]\frac{1}{x-2}[/latex]
[latex]\frac{1}{x-2}=0[/latex]
[latex]x=2[/latex]
So this tells us that $2$ is not in the domain of this function. There are no other numbers that will make the denominator equal 0, so we write the domain to exclude just 2.
Domain: [latex](-\infty,2)\bigcup(2,+\infty)[/latex]
To find the horizontal asymptote, notice how [latex]\frac{1}{x-2}[/latex] will get smaller and smaller as [latex]x[/latex] increases. This part of [latex]g(x)[/latex] will approach 0. Now looking at the whole function [latex]g(x)=\frac{29}{53}+\frac{1}{x-2}[/latex], if the second term is approaching 0, then what is left, that is not changing, is the horizontal asymptote [latex]y=\frac{29}{53}[/latex].
c.
[latex]11x-7=0[/latex]
[latex]x=\frac{7}{11}[/latex]
So this tells us that [latex]\frac{7}{11}[/latex] is not in the domain of this function. There are no other numbers that will make the denominator equal 0, so we write the domain to exclude just [latex]\frac{7}{11}[/latex].
Domain: [latex](-\infty, \frac{7}{11})\bigcup(\frac{7}{11},+\infty)[/latex]
To find the horizontal asymptote, identify the leading term (and degree) of the numerator and denominator. Numerator: [latex]-13x[/latex] and Denominator: [latex]11x[/latex].
Since these have the same degree, look at each term’s coefficient. This leads to a horizontal asymptote of [latex]y=-\frac{13}{11}[/latex].
d.
[latex]537(x+5)(x+1)(x^2+1)(x-15)=0[/latex]
[latex]x=-5, -1, 15[/latex]
[latex]x^2+1=0[/latex] does not have any real solutions. This tells us that -5, -1 and 15 are not in the domain of this function. There are no other numbers that will make the denominator equal 0, so we write the domain to exclude just those three values.
Domain: [latex](-\infty, -5)\bigcup(-5,-1)\bigcup (-1,15)\bigcup(15,+\infty)[/latex]
To find the horizontal asymptote, identify the leading term (and degree) of the numerator and denominator. Numerator: [latex]151x^4[/latex] and Denominator: [latex]537x^5[/latex].
Since the denominator’s degree is larger, the horizontal asymptote is [latex]y=0[/latex].