5.3 Modeling with polynomial functions
Activity 5.3.2
According to a shipping company's regulations, the girth plus the length of a parcel they transport for their lowest rate may not exceed 120 inches, where by girth we mean the perimeter of the smallest end.
Suppose that we want to ship a parcel that has a square end of width [latex]x[/latex] and an overall length of [latex]y[/latex], both measured in inches.
a. Label the provided picture, using [latex]x[/latex] for the length of each side of the square end, and [latex]y[/latex] for the other edge of the package.
b. How does the length plus girth of 120 inches result in an equation (often called a constraint equation) that relates [latex]x[/latex] and [latex]y[/latex]? Explain, and state the equation.
c. Solve the equation you found in (b) for one of the variables present.
d. Hence determine the volume, [latex]V[/latex], of the package as a function of a single variable.
e. What is the domain of the function [latex]V[/latex] in the context of the physical setting of this problem? (Hint: what's the maximum value of [latex]x[/latex]? the maximum value of [latex]y[/latex]?)
Show Solution
a. 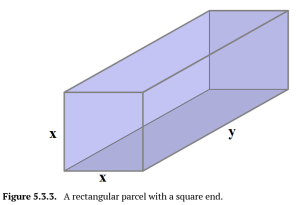
b. [latex]4x+y=120[/latex], because the girth, the perimeter of the smallest side is [latex]4x[/latex], then add the length [latex]y[/latex] for a total of 120.
c. [latex]y=120-4x[/latex]
d. Recall that the volume can be found by multiplying length, width and height. Width and height are each [latex]x[/latex], and length [latex]y[/latex] is rewritten as [latex]120-4x[/latex], so [latex]V=x^2(120-4x)[/latex].
e. The domain is [latex](0,30)[/latex], because there must be some positive value of [latex]x[/latex] for a parcel to exist, but the domain must be less than 30, so as not to exceed the shipping regulation of girth plus length not being more than 120 inches.
5.3 Exercise 5
Suppose that we want a cylindrical barrel to hold 8 cubic feet of volume. Let the barrel have radius [latex]r[/latex] and height [latex]h[/latex], each measured in feet. How can we write the surface area, [latex]A[/latex], of the barrel solely as a function of [latex]r[/latex]?
a. Draw several possible pictures of how the barrel might look. For instance, what if the radius is very small? How will the height appear in comparison? Likewise, what happens if the height is very small?
b. Use the fact that volume is fixed at 8 cubic feet to state a constraint equation and solve that equation for [latex]h[/latex] in terms of [latex]r[/latex].
c. Recall that the surface area of a cylinder is [latex]A=2\pi r^2+2\pi rh[/latex]. Use your work in (c) to write [latex]A[/latex] as a function of only [latex]r[/latex].
d. What is the domain of [latex]A[/latex]? Why?
e. Explain why [latex]A[/latex] is not a polynomial function of [latex]r[/latex].
Show Solution
a. INSERT hand drawings here. If the radius is small, then the height is big.. Conversely, if the height is small, then the radius is big.
b. If the volume is 8 cubic feet, and [latex]V=\pi r^2h[/latex], then [latex]8=\pi r^2h[/latex]. Solving this for [latex]h[/latex] gives: [latex]h=\frac{8}{\pi r^2}[/latex].
c. In the surface area formula, we will substitute for [latex]h[/latex] and get [latex]A=2\pi r^2+2\pi r \cdot \frac{8}{\pi r^2}[/latex].
d. [latex](0,\infty)[/latex], because the radius has to be a positive value, and, though impractical, can get very very large.
e. Because the polynomial form can only have positive exponents, and [latex]A[/latex] has a term with a negative exponent.
