4.5 Other Trigonometric Functions and Identities

If we know that [latex]\sec(\beta) = -2[/latex], it follows that[latex]\cos(\beta) = \frac{-1}{2}[/latex]. Now, we can view [latex]\beta[/latex] as an angle in a right triangle in quadrant [latex]II[/latex]. So, the adjacent side is [latex]-1[/latex] and the hypotenuse is [latex]2[/latex].

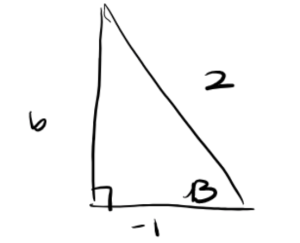
Then we can solve for the missing side in the right triangle using the pythagorean theorem. We have that [latex](-1)^2 + b^2 = (2)^2[/latex] which simplifies to [latex]1 + b^2 = 4[/latex]. Isolating b we get that [latex]b = \sqrt{3}[/latex]. Now that we have all the sides of the right triangle we can now find the values of the other five trigonometric functions using their right triangle definitions to get 

• [latex]\cos(\beta) = \frac{-1}{2}[/latex]
• [latex]\sin(\beta) = \frac{\sqrt{3}}{2}[/latex]
• [latex]\tan(\beta) = -\frac{\sqrt{3}}{1}[/latex]
• [latex]\csc(\beta) = \frac{2}{\sqrt{3}}[/latex]
• [latex]\cot(\beta) = -\frac{1}{\sqrt{3}}[/latex]

We start by drawing a right triangle with the given information.

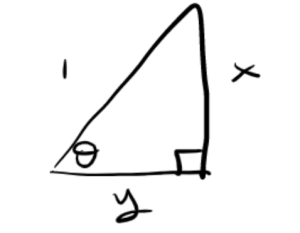
Now, we want to find the missing side length [latex]y[/latex] in terms of [latex]x[/latex]. We start with the Pythagorean theorem. So we know that [latex]x^2+y^2 = 1^2[/latex]. Moving [latex]x^2[/latex] over we get [latex]y^2 = 1 - x^2[/latex]. Now we take the square root of both sides to solve for y to get that [latex]y = \sqrt{1-x^2}[/latex]. Now all of our sides are in terms of [latex]x[/latex]. Next, we use the right triangle definitions of the trigonometric functions to find the missing quantities.

1. [latex]\sin(\theta) = \frac{x}{1} [/latex]
2. [latex]\sec(\theta) = \frac{1}{y} = \frac{1}{\sqrt{1-x^2}}[/latex]
3. [latex]\csc(\theta) = \frac{1}{x}[/latex]
4. [latex]\tan(\theta) = \frac{x}{y} = \frac{x}{\sqrt{1-x^2}}[/latex]
5. We first will make note that if [latex]\sin(\theta) = \frac{x}{1}[/latex], then using inverse trig we can say that [latex]\arcsin(x) = \theta[/latex]. So then we have [latex]\cos(\arcsin(x)) = \cos(\theta) = \frac{y}{1} = \frac{\sqrt{1-x^2}}{1}[/latex].
6. In a similar process as e, we know that [latex]\arcsin(x) = \theta[/latex]. So, [latex]\cot(\arcsin(x))  = \cot(\theta) = \frac{y}{x} = \frac{\sqrt{1-x^2}}{x}[/latex].