4.4 Finding Angles

a. We first draw our picture.

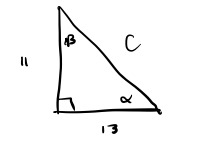
To determine the measure of [latex]\beta[/latex] we use the right triangle definition of tangent: [latex]\tan(\beta) = \frac{opp}{adj}[/latex]. So we have that [latex]\tan(\beta) = \frac{13}{11}[/latex]. Now we can rewrite this statement using the inverse function notation to get [latex]\beta = \arctan(\frac{13}{11}) = \approx 0.866[/latex].

Next, we determine the measure of [latex]\alpha[/latex] similarly. We first start with the triangle definition of tangent to get [latex]\tan(\alpha) = \frac{11}{13}[/latex]. Rewriting using inverse notation we get [latex]\alpha = \arctan(\frac{11}{13}) \approx 0.702[/latex].

Finally, we determine the length of the hypotenuse [latex]c[/latex] by using the pythagorean theorem: [latex]c^2 = 11^2+13^2 = 290[/latex]. So, [latex]c = \sqrt{290}[/latex].

b. First we draw the picture.

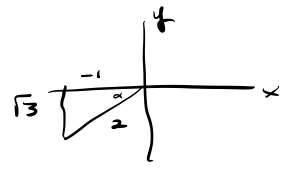
Note that we are given [latex]\cos(\alpha) = \frac{-1}{2}[/latex]. So, that means the [latex]\frac{-1}{2}[/latex] is the [latex]x[/latex]-distance of our corresponding right triangle with angle [latex]\alpha[/latex]. So, we first solve for [latex]\alpha[/latex]. We have [latex]\cos(\alpha) = \frac{-1}{2}[/latex]. We want to determine the angle that gives us a cosine value of [latex]\frac{-1}{2}[/latex]and our angle is in quadrant  II. Using our unit circle [latex]\alpha = \frac{2\pi}{3}[/latex]. Now we determine [latex]sin(\frac{2\pi}{3}) = \sqrt{3}{2}[/latex].

c. We will do this problem using two methods:

Method 1: Unit Circle Method

First we draw a picture. that sin(\beta) = 0.1. So our angle [latex]\beta[/latex] has a [latex]y[/latex]-coordinate of [latex]0.1[/latex] on the unit circle.

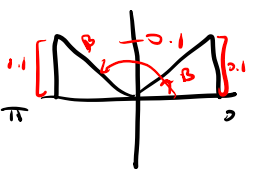
Note if we solve for [latex]\beta[/latex] using inverses we get [latex]\beta = \sin(0.1)[/latex]. However, this is not the angle we are looking for. We recall that the range of arcsine is in the interval [latex][-\frac{\pi}{2}, \frac{\pi}{2}][/latex]. There are actually two angles that correspond so that it the [latex]y[/latex]-distance of our  right triangle with angle \beta. So, we [latex]\beta = \sin(0.1)[/latex] is our angle in quadrant 1. We want to determine the corresponding angle in quadrant II. So we can note that if we subtract our angle [latex]\sin(0.1)[/latex] from [latex]\pi[/latex] that will get us the corresponding angle in quadrant II as seen below.

So, our angle [latex]\beta[/latex] in quadrant II is [latex]\beta = \pi - \sin(0.1) \approx 3.04[/latex] radians.

Finally we find [latex]\cos(\beta) = \cos(\pi-arcos(0.1)) \approx -0.995[/latex] radians.

Method 2: Using a Graph.

In our second method to solve this problem we will first start our by drawing a graph of the sine curve.

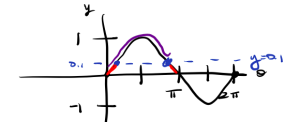
First, we make note we are trying to solve [latex]sin(\beta) = 0.1[/latex]. So, we will draw a vertical line at [latex]y = 0.1[/latex]. There are two spots on our graph that has a y-coordinate of [latex]0.1[/latex]. Our horizontal distance on the graph are the angles. The angles represent how far we have traveled along the curve. Using inverse trig our first angle is [latex]\beta = \sin(0.1)[/latex]. This angle is in quadrant I. We want to find the angle in quadrant II which is the second distance traveled on our graph (in blue). Note, that if we subtract [latex]\beta[/latex] from [latex]\pi[/latex] that is our second angle. Thus, the measure of angle \beta in quadrant II is  [latex]\beta = \pi - arcsin(0.1)[/latex].

First, we draw a picture of the scenario.

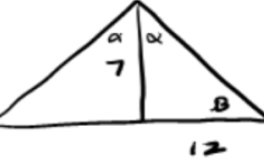
We first want to determine the measure of the angle the roof makes with the horizontal. That is angle [latex]\beta[/latex] in our diagram. So, we will determine the measure of [latex]\beta[/latex] using the tangent definition of a right triangle. We have [latex]\tan(\beta) = \frac{7}{12}[/latex].

We can rewrite this statement using inverse functions to get

[latex]\beta = \arctan(\frac{7}{12})[/latex].

Now putting this into desmos to get the approximate measure we get [latex]\beta \approx 30.26^{\circ}[/latex].

Next, we want to determine the measure of the angle at the peak of the roof. Let’s call this angle ‘[latex]x[/latex]‘. In our diagram [latex]x = \alpha + \alpha = 2\alpha[/latex]. So, we will first determine the measure of [latex]\alpha[/latex]. We know that the sum of the angles in a right triangle have to add to [latex]180^{\circ}[/latex]. Also, our right angle already has a measure of [latex]90^{\circ}[/latex] so  [latex]\alpha + \beta  = 90^{\circ}[/latex].

Solving for [latex]\alpha[/latex] we get [latex]\alpha = 90 - \beta = 90 - \arctan(\frac{7}{12})[/latex]. Now we plug in [latex]\alpha[/latex] to find [latex]x[/latex] to get:

[latex]x = 2\alpha = 2(90 - \arctan(\frac{7}{12}))  = 180 - 2\arctan(\frac{7}{12}) \approx 119.487^{\circ}[/latex].

Therefore, the angle at the peak of the roof has a measure of [latex]119.487^{\circ}.[/latex]