4.1 Right Triangles

a.

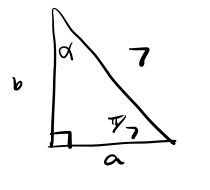
We first solve for missing angle [latex]\alpha[/latex]. To determine [latex]\alpha[/latex] we use the fact that the angles add up to [latex]\pi[/latex] radians. So, [latex]\alpha = \frac{\pi}{2} - \frac{\pi}{7}  = \frac{7\pi - 2\pi}{14} = \frac{5\pi}{14}[/latex].

Now we solve for the missing sides. Using the right triangle definition of sine we get  [latex]7\sin(\frac{\pi}{7}) = \frac{b}{7}[/latex]. Multiplying by [latex]7[/latex]on both sides gives [latex]b = 7\sin(\frac{\pi}{7}) \approx 3.04[/latex].

Similarly to solve for a we use the right triangle definition of cosine to get [latex]\cos(\frac{\pi}{7}) = \frac{a}{7}[/latex]. Multiplying by [latex]7[/latex] on both sides we get [latex]a = 7\cos(\frac{\pi}{7}) \approx 6.31[/latex].

b.

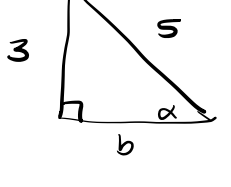
Given that [latex]\sin(\alpha) = \frac{3}{5}[/latex], we cannot determine the missing angle \alpha since [latex]\frac{3}{5}[/latex] is not of our special values on the unit circle. Later, we will learn how to solve for missing angles. But for now, in order to determine the remaining angles we need to know the measure of at least one non-right angle and one side and we only know the length of the right angle.

But we can find the missing side since [latex]\sin(\alpha) = \frac{3}{5}[/latex]. then we know in our right triangle that [latex]3[/latex] is the length of the opposite side and [latex]5[/latex] is the length of the hypotenuse. Now we can solve for the missing side [latex]b[/latex] using the pythagorean theorem. So we have

\begin{align*}
3^2+b^2 & = 5^2 \\
9 + b^2 & = 25 \\
b^2  & = 16 \\
b & = 4 \\
\end{align*}

c.

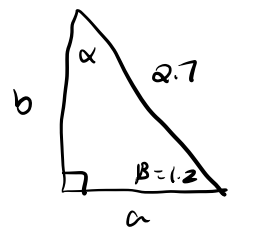
First we solve for [latex]\alpha[/latex] and get [latex]\alpha = \frac{\pi}{2} - 1.2 \approx 0.37[/latex].

Now we solve for missing side [latex]b[/latex] using the definition of sine with right triangles: [latex]\sin(1.2) = \frac{b}{2.7}[/latex]. Multiplying both sides by [latex]2.7[/latex] we get [latex]b = 2.7\sin(1.2) \approx 2.52[/latex].

Finally, we solve for side [latex]a[/latex] using the definition of cosine with right triangles to get: [latex]\cos(1.2) = \frac{a}{2.7}[/latex]. Multiplying both sides by [latex]2.7[/latex] we get [latex]c = 2.7\cos(1.2) \approx 0.98[/latex].

d.

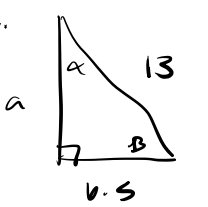
We find the missing side [latex]a[/latex] using the Pythagorean theorem. We get,

\begin{align*}
a^2 + (6.5)^2 & = 13^2 \\
a^2 + 42.25 & = 169 \\
a^2 & = 126.75 \\
a & \approx 11.25 \\
\end{align*}

Using the right triangle definition of sine we get [latex]\sin(\alpha) = \frac{6.5}{13} = \frac{1}{2}[/latex]. We are looking for the angle that gives us a sine value of [latex]\frac{1}{2}[/latex] which is one of our special values on the unit circle. So we know [latex]\alpha = \frac{\pi}{6}[/latex]. Now using the fact that all angles in a right triangle must add up to \pi we solve for [latex]\beta[/latex] to get: [latex]\beta = \frac{\pi}{2} - \frac{\pi}{6} = \frac{3\pi}{6} - \frac{\pi}{6} = \frac{\pi}{3}[/latex].

e.

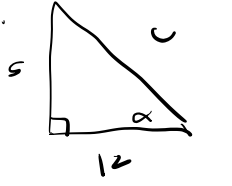
We first solve for the length of the hypotenuse using the pythagorean theorem. So we have,

[latex]c^2 = 5^2+12^2 = 169[/latex]. So [latex]c = \sqrt{169} = 13[/latex]. If we set up our trigonometric ratio to solve for the missing angle we get [latex]\sin(\alpha) = \frac{5}{13}[/latex]. We cannot find the missing angles because we are not given one of the special values on the unit circle and we do not know how to solve for [latex]\alpha[/latex] just yet. So, since we do not have a non right angle we can only find the missing side.

f.

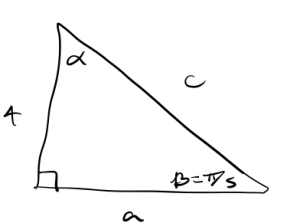
First we find the missing angle [latex]\alpha = \frac{\pi}{2} - \frac{\pi}{5} = \frac{5\pi}{10} - \frac{2\pi}{10} = \frac{3\pi}{10}[/latex].

Now to find the missing sides, we start with [latex]\sin(\frac{\pi}{5}) = \frac{4}{c}[/latex]. Multiplying both sides by [latex]c[/latex] we get

[latex]c = 4\sin(\frac{\pi}{5}) \approx 2.35[/latex].

Now to find the measure of [latex]a[/latex] we will use the right triangle definition of cosine to get [latex]\cos(\frac{\pi}{5}) = \frac{a}{c}[/latex]. Solving for [latex]a[/latex] we get [latex]a = c \cdot \cos(\frac{\pi}{5}) = 4\sin(\frac{\pi}{5}) \approx 1.90.[/latex].