3.3 The special number e
Activity 3.3.3
By graphing [latex]f(t) = e^t[/latex] and appropriate horizontal lines, estimate the solution to each of the following equations. Note that in some parts, you may need to do some algebraic work in addition to using the graph.
a. [latex]e^t=2[/latex]
b. [latex]e^{3t}=5[/latex]
c. [latex]2e^4-4=7[/latex]
d. [latex]3e^(0.25)^t+2=6[/latex]
e. [latex]4-2e^{-0.7t}=3[/latex]
f. [latex]2e^{1.2t}=1.5e^{1.6t}[/latex]
Show Solution
a. We want to find the input that would give [latex]2[/latex] as an output. We first start by drawing a graph of [latex]f(t) = e^t[/latex] in desmos and the horizontal line [latex]y = 2[/latex].
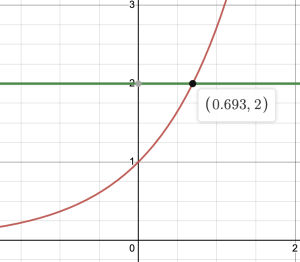
Using the graph this gives an input of about [latex]0.693[/latex]. So [latex]t \approx 0.693.[/latex]
b. We want to find the input that would give [latex]5[/latex] as an output. We start by drawing a graph of [latex]f(t) = e^t[/latex] in desmos and the horizontal line [latex]y = 5[/latex].
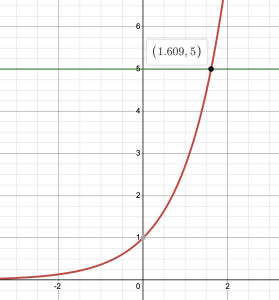
Based off the graph of [latex]e^t[/latex], this input is about [latex]1.609[/latex]. In our case our input is [latex]3t[/latex] so we have that [latex]3t = 1.609[/latex]. Dividing both sides by [latex]3[/latex] gives [latex]t \approx 0.563[/latex].
c. We will first do some algebra to get [latex]e^t[/latex] by itself on one side so we can use the graph to find a solution:
\begin{align*}
2e^t-4 & = 7 \\
2e^t & = 11 \\
e^t & = \frac{11}{2} \\
\end{align*}
So we want to determine the input that gives an output of [latex]\frac{11}{2}[/latex]. We draw the graph of [latex]f(t) = e^t[/latex] and the horizontal line [latex]y = \frac{11}{2}[/latex] in desmos.
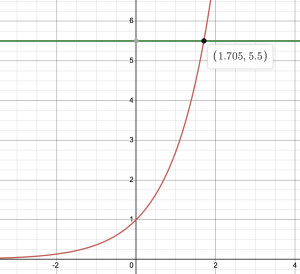
Based off the graph, the input is [latex]1.705[/latex]. So, [latex]t \approx 1.705[/latex].
d. We will first do some algebra to get the exponential term by itself on one side so we can use the graph to find a solution:
\begin{align*}
3e^{0.25t}+2 &=6 \\
3e^{0.25t} & = 4 \\
e^{0.25t} & = \frac{4}{3}
\end{align*}
So we want to determine the input that gives an output of [latex]\frac{4}{3}[/latex]. We draw the graph of [latex]f(t) = e^t[/latex] and the horizontal line [latex]y = \frac{4}{3}[/latex] in desmos.
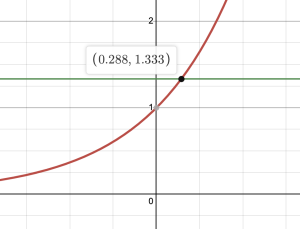
Based off the graph of [latex]e^t[/latex], the input is [latex]0.288[/latex]. In the case of our function the input is [latex]0.25t[/latex]. So, [latex]0.25t = 0.288[/latex]. Dividing both sides by [latex]0.25[/latex] gives [latex]t \approx 1.152.[/latex]
e. We will first do some algebra again to isolate the exponential term:
\begin{align*}
4-2e^{-0.7t} & =3 \\
-2e^{-0.7t} & = -1 \\
e^{-0.7t} & = \frac{1}{2} \\
\end{align*}
So we want to determine the input that gives an output of [latex]\frac{1}{2}[/latex]. We draw the graph of [latex]f(t)=e^t[/latex] and the horizontal line [latex]y = \frac{1}{2}[/latex]in desmos.
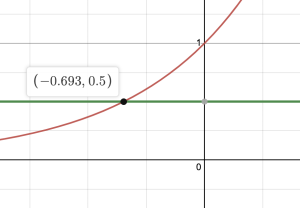
Based off the graph of [latex]e^t[/latex], the input is [latex]-0.693[/latex]. In the case of our function the input is [latex]-0.7t[/latex]. So, [latex]-0.7t = -0.693[/latex]. Dividing both sides by [latex]-0.7[/latex] to solve for t we get [latex]t \approx 0.99[/latex].
f. We will again do some algebra to isolate the exponential term:
[latex]2e^{1.2t} = 1.5e^{1.6t}[/latex]
We will first divide both sides by [latex]e^{1.2t}[/latex].
[latex]2 = \frac{1.5e^{1.6t}}{e^{1.2t}}[/latex].
Using exponential rules, when we divide by the same base we subtract the exponents:
[latex]2 = 1.5e^{0.4t}[/latex].
Finally, we divide both sides by 1.5 to get [latex]e^{0.4t} = \frac{2}{1.5} = \frac{2}{3/2} = 2 \cdot \frac{2}{3} = \frac{4}{3}[/latex].
So we want to determine the input that gives an output of [latex]\frac{4}{3}[/latex]. We draw the graph of [latex]f(t) = e^t[/latex] and the horizontal line [latex]y = \frac{4}{3}[/latex] in desmos.

Based off the graph of [latex]e^t[/latex], the input is [latex]0.288[/latex]. In the case of our function our input is [latex]0.4t[/latex]. So, [latex]0.4t = 0.288[/latex]. Dividing both sides by [latex]0.4[/latex] to solve for [latex]t[/latex] we get [latex]t \approx 0.72[/latex].
