2.3 The Sine and Cosine Functions
Let [latex]k=g(t)[/latex] be the function that tracks the [latex]x[/latex]-coordinate of a point traversing the unit circle counterclockwise from [latex](1,0)[/latex]. That is, [latex]g(t)=\cos (t)[/latex]. Use the information we know about the unit circle that is summarized in Figure 2.3.1 to respond to the following questions.
a. What is the exact value of [latex]\cos (\frac{\pi}{6})[/latex]? of [latex]\cos (\frac{5\pi}{6})[/latex]? [latex]\cos (-\frac{\pi}{3})[/latex]?
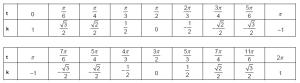
b. Complete the following table with the exact values of[latex]k[/latex] that correspond to the stated inputs.

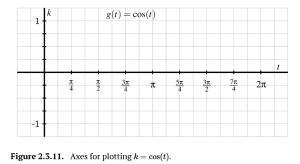
c. On the axes provided in Figure 2.3.11, sketch an accurate graph of [latex]k=\cos (t)[/latex]. Label the exact location of several key points on the curve.
d. What is the exact value of [latex]\cos (\frac{11\pi}{4})[/latex]? of [latex]\cos (\frac{14\pi}{3})[/latex]
e. Give four different values of [latex]t[/latex] for which [latex]\cos (t)=-\frac{\sqrt{3}}{2}[/latex].
f. How is the graph of [latex]k=\cos (t)[/latex] different from the graph of [latex]h=\sin (t)[/latex]? How are the graphs similar?
Show Solution
a. [latex]\cos (\frac{\pi}{6})=\frac{ \sqrt{3} }{2}[/latex], [latex]\cos (\frac{5\pi}{6})=-\frac{ \sqrt{3} }{2}[/latex], [latex]\cos (-\frac{\pi}{3})=\frac{1}{2}[/latex]
b.
c.
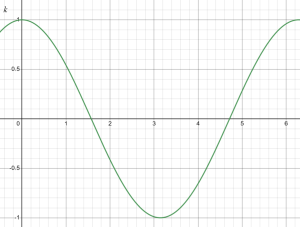
d. [latex]\cos (\frac{11\pi}{4})=\cos (\frac{3\pi}{4})=-\frac{\sqrt{2}}{2}[/latex]
[latex]\cos (\frac{14\pi}{3})=\cos (\frac{2\pi}{3})=-\frac{1}{2}[/latex]
e. For [latex]\cos (t)=-\frac{\sqrt{3}}{2}[/latex], [latex]t=\frac{5\pi}{6}, \frac{7\pi}{6}, \frac{17\pi}{6}, \frac{19\pi}{6}[/latex].
f. Graph [latex]k[/latex] and Graph [latex]h[/latex] both have the same amplitude, same period and same midline, but they are horizontal shifts of each other, resulting in different [latex]y[/latex]-intercepts.
Answer the following questions exactly wherever possible. If you estimate a value, do so to at least 5 decimal places of accuracy.
a. The [latex]x[/latex]-coordinate of the point on the unit circle that lies in the third quadrant and whose y-coordinate is [latex]y=-34[/latex].
b. The [latex]y[/latex]-coordinate of the point on the unit circle generated by a central angle in standard position that measures [latex]t=2[/latex] radians.
c. The [latex]x[/latex]-coordinate of the point on the unit circle generated by a central angle in standard position that measures [latex]t=-3.05[/latex] radians.
d. The value of [latex]\cos (t)[/latex] where [latex]t[/latex] is an angle in Quadrant II that satisfies [latex]\sin (t)=12[/latex].
e. The value of [latex]\sin (t)[/latex] where [latex]t[/latex] is an angle in Quadrant III for which [latex]\cos (t)=-0.7[/latex].
f. The average rate of change of [latex]f(t)=\sin (t)[/latex] on the intervals [latex][0.1,0.2][/latex] and [latex][0.8,0.9][/latex].
g. The average rate of change of [latex]g(t)=\cos (t)[/latex] on the intervals [latex][0.1,0.2][/latex] and [latex][0.8,0.9][/latex].
Show Solution
a. Use Pythagorean Theorem.
[latex]x^2+(-\frac{3}{4})^2=1[/latex]
[latex]x^2+\frac{9}{16}=1[/latex]
[latex]x^2=\frac{7}{16}[/latex]
[latex]x=-\frac{\sqrt{7}}{4}[/latex]
NOTE: when you take the square root of [latex]\frac{7}{16}[/latex], you get both a positive and negative answer. BUT, this point is in the third quadrant, so the [latex]x[/latex]-coordinate must be negative.
b. Since we know the angle is [latex]2[/latex] radians, the [latex]y[/latex]-coordinate is [latex]\sin (2) \approx 0.90930[/latex].
c. Since we know the angle is [latex]-3.05[/latex] radians, the [latex]x[/latex]-coordinate is [latex]\cos (-3.05) \approx -0.99581[/latex].
d. In Quadrant II, [latex]\sin (t)=\frac{1}{2}[/latex] when [latex]t=\frac{5\pi}{6}[/latex].
[latex]\cos (\frac{5\pi}{6})=-\frac{\sqrt{3}}{2}[/latex].
e. Use [latex]\cos^2 (t)+\sin^2 (t)=1.[/latex]
If [latex]cos (t)=-.7,[/latex]then [latex]\sin^2 (t)+(-.7)^2=1[/latex].
[latex]\sin^2 (t)=.51[/latex]
[latex]\sin (t)=-\sqrt{.51}[/latex]
NOTE: [latex]\sin (t)[/latex] is negative, because the coordinate is in Quadrant III.
f. SKIP
g. SKIP
