1.9 Combining Functions
Activity 1.9.2
Consider the functions [latex]f[/latex] and [latex]g[/latex] defined by Figure 1.94. and Figure 1.9.5.
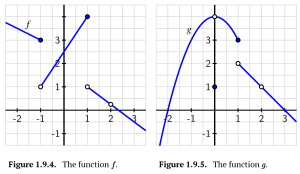
a. Determine the exact value of [latex](f+g)(0)[/latex].
b. Determine the exact value of [latex](g-f)(1)[/latex].
c. Determine the exact value of [latex](f\cdot g)(-1)[/latex].
d. Are there any values for [latex]x[/latex] for which [latex](\frac{f}{g})(x)[/latex] is undefined? If not, explain why. If so, determine the values and justify your answer.
e. For what values of [latex]x[/latex] is [latex](f\cdot g)(x)=0[/latex]? Why?
f. Are there any values of [latex]x[/latex] for which [latex](f-g)(x)=0[/latex]? Why or why not?
Show Solution
a. [latex](f+g)(0)=f(0)+g(0)=2.5+1=3.5[/latex]
b. [latex](g-f)(1)=g(1)-f(1)=3-4=-1[/latex].
c. [latex](f\cdot g)(-1)=f(-1)\cdot g(-1)=3\cdot 3=9[/latex].
d. [latex](\frac{f}{g})(x)=\frac{f(x)}{g(x)}[/latex], so when [latex]g(x)=0[/latex], this will be undefined. So [latex]x=-2, 3[/latex]. Also, [latex]g(x)[/latex] is not defined at [latex]x=2.[/latex]
e. [latex](f\cdot g)(x)=0[/latex] is the same as [latex]f(x)\cdot g(x)=0[/latex]. If either [latex]f(x)=[/latex] or [latex]g(x)=0[/latex], then [latex](f\cdot g)(x)=0[/latex]. [latex]x= -2, 3[/latex] and [latex]x \approx 2.4[/latex].
Activity 1.9.4
In what follows, we work to understand two different piecewise functions entirely by hand based on familiar properties of linear and quadratic functions.
a. Consider the function [latex]p[/latex] defined by the following rule:
[latex]p(x)=\begin{cases} -(x+2)^2+2 & x < 0 \\ \frac{1}{2}(x-2)^2+1 & x\geq 0 \end{cases}[/latex]
What are the values of [latex]p(-4), p(-2), p(0), p(2)[/latex], and [latex]p(4)[/latex]?
b. What point is the vertex of the quadratic part of [latex]p[/latex] that is valid for [latex]x<0[/latex]? What point is the vertex of the quadratic part of [latex]p[/latex] that is valid for [latex]x \geq 0[/latex]?
c. For what values of [latex]x[/latex] is [latex]p(x)=0[/latex]? In addition, what is the [latex]y[/latex]-intercept of [latex]p[/latex]?
d. Sketch an accurate, labeled graph of [latex]y=p(x)[/latex] on the axes provided in Figure 1.9.9.
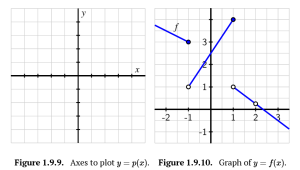
e. For the function [latex]f[/latex] defined by Figure 1.9.10, determine a piecewise-defined function formula for [latex]f[/latex] that is expressed in bracket notation similar to the definition of [latex]y=p(x)[/latex] above.
Show Solution
a. [latex]p(-4)=-(-4+2)^2+2=-2[/latex]
[latex]p(-2)=-(-2+2)^2+2=2[/latex]
[latex]p(0)=\frac{1}{2}(0-2)^2+1=3[/latex]
[latex]p(2)=\frac{1}{2}(2-2)^2+1=1[/latex]
[latex]p(4)=\frac{1}{2}(4-2)^2+3=[/latex]
b. Left vertex: [latex](-2,2)[/latex]. Right vertex: [latex](2,1)[/latex]
c. [latex]p(x)=0[/latex] is only relevant for the left piece as the right piece never hits 0. So
[latex]-(x+2)^2+2=0[/latex]
[latex](x+2)^2=2[/latex]
[latex]x=-2-\sqrt{2}, -2+\sqrt{2}[/latex]
The [latex]y[/latex]-intercept is [latex](0,3)[/latex].
d.
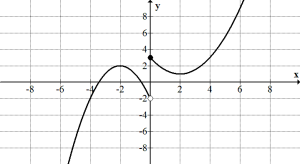
e. [latex]p(x)=\begin{cases} -0.5x+2.5 & x \leq -1 \\ 1.5x+2.5 & -1 < x \leq 1 \\ -0.75x+1.75 & 1 < x \leq 2 \\ -0.75x+1.75 & 2 < x \end{cases}[/latex]
