1.8 Transformation of Functions
Activity 1.8.2 ab
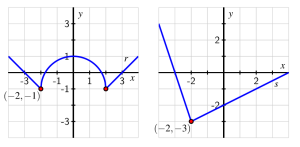
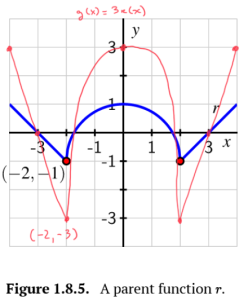
Consider the functions [latex]r[/latex] and [latex]s[/latex] given in Figure 1.8.5 and Figure 1.8.6.
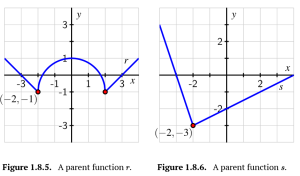
a. On the same axes as the plot of [latex]y=r(x)[/latex], sketch the following graphs: [latex]y=g(x)=r(x)+2, y=h(x)=r(x+1)[/latex], and [latex]y=f(x)=r(x+1)+2[/latex]. Be sure to label the point on each of [latex]g, h[/latex], and [latex]f[/latex] that corresponds to [latex](−2,−1)[/latex] on the original graph of [latex]r[/latex]. In addition, write one sentence to explain the overall transformations that have resulted in [latex]g, h[/latex], and [latex]f[/latex].
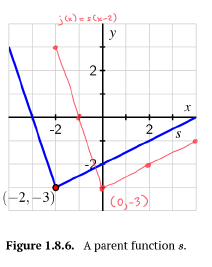
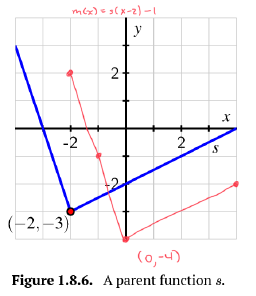
b. On the same axes as the plot of [latex]y=s(x)[/latex], sketch the following graphs: [latex]y=k(x)=s(x)−1, y=j(x)=s(x−2)[/latex], and [latex]y=m(x)=s(x−2)−1[/latex]. Be sure to label the point on each of [latex]k, j[/latex], and [latex]m[/latex] that corresponds to [latex](−2,−3)[/latex] on the original graph of [latex]r[/latex]. In addition, write one sentence to explain the overall transformations that have resulted in [latex]k, j[/latex], and [latex]m[/latex].
c. Now consider the function [latex]q(x)=x^2[/latex]. Determine a formula for the function that is given by [latex]p(x)=q(x+3)−4[/latex]. How is [latex]p[/latex] a transformation of [latex]q[/latex]?
Show Solution
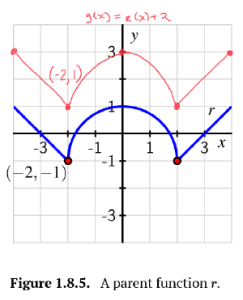
a. [latex]y=g(x)=r(x)+2[/latex]: The graph of [latex]r[/latex] has been shifted up 2 units.
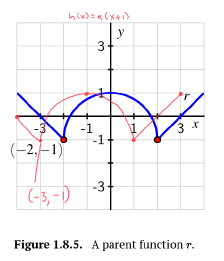
[latex]y=h(x)=r(x+1)[/latex]: The graph of [latex]r[/latex] has been shifted 1 unit to the left.
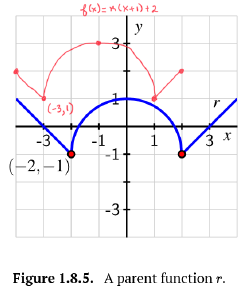
[latex]y=f(x)=r(x+1)+2[/latex]: The graph of [latex]r[/latex] has been shifted 1 unit to the left AND shifted up 2 units.
b. [latex]y=k(x)=s(x)−1[/latex]: The graph of [latex]s[/latex] has been shifted down 1 unit.
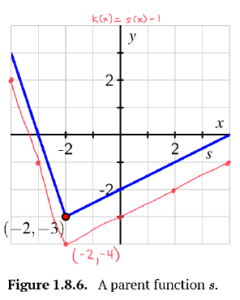
[latex]y=j(x)=s(x−2)[/latex]: The graph of [latex]s[/latex] has been shifted 2 units to the right.
[latex]y=m(x)=s(x−2)−1[/latex]: The graph of [latex]s[/latex] has been shifted 2 units to the right AND shifted down 1 unit.
c. SKIP
Activity 1.8.3 ab
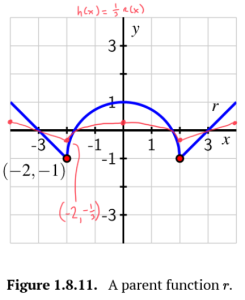
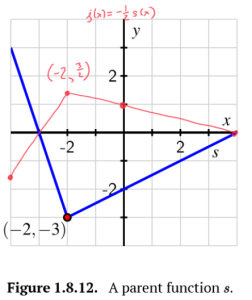
Consider the functions [latex]r[/latex] and [latex]s[/latex] in Figure 1.8.11 and Figure 1.8.12.
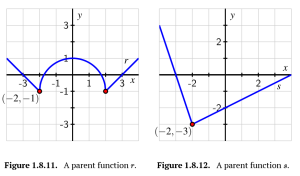
a. On the same axes as the plot of [latex]y=r(x)[/latex], sketch the following graphs: [latex]y=g(x)=3r(x)[/latex] and [latex]y=h(x)=\frac{1}{3}r(x)[/latex]. Be sure to label several points on each of [latex]r, g[/latex], and [latex]h[/latex] with arrows to indicate their correspondence. In addition, write one sentence to explain the overall transformations that have resulted in [latex]g[/latex] and [latex]h[/latex] from [latex]r[/latex].
b. On the same axes as the plot of [latex]y=s(x)[/latex], sketch the following graphs: [latex]y=k(x)=−s(x)[/latex] and [latex]y=j(x)=−\frac{1}{2}s(x)[/latex]. Be sure to label several points on each of [latex]s, k[/latex], and [latex]j[/latex] with arrows to indicate their correspondence. In addition, write one sentence to explain the overall transformations that have resulted in [latex]k[/latex] and [latex]j[/latex] from [latex]s[/latex].
c. On the additional copies of the two figures below, sketch the graphs of the following transformed functions: [latex]y=m(x)=2r(x+1)−1[/latex] (at left) and [latex]y=n(x)=\frac{1}{2}s(x−2)+2[/latex]. As above, be sure to label several points on each graph and indicate their correspondence to points on the original parent function.
d. Describe in words how the function [latex]y=m(x)=2r(x+1)−1[/latex] is the result of three elementary transformations of [latex]y=r(x)[/latex]. Does the order in which these transformations occur matter? Why or why not?
Show Solution
a. [latex]y=g(x)=3r(x)[/latex]: The graph of [latex]r[/latex] has been vertically stretched by 3.
[latex]y=h(x)=\frac{1}{3}r(x)[/latex]: The graph of [latex]r[/latex] has been vertically compressed by a factor of 3.
b. [latex]y=k(x)=−s(x)[/latex]: The graph of [latex]s[/latex] has been reflected across the horizontal axis.
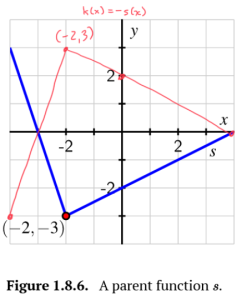
[latex]y=j(x)=−\frac{1}{2}s(x)[/latex]: The graph of [latex]s[/latex] has been reflected across the horizontal axis AND vertical compressed by a factor of 2.
c. SKIP
d. SKIP
Activity 1.8.4
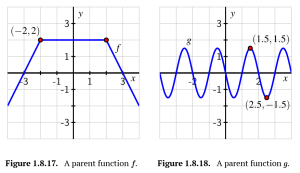
Consider the functions [latex]f[/latex] and [latex]g[/latex] given in Figure 1.8.17 and Figure 1.8.18.
a. Sketch an accurate graph of the transformation [latex]y=p(x)=−\frac{1}{2}f(x−1)+2.[/latex] Write at least one sentence to explain how you developed the graph of [latex]p[/latex], and identify the point on [latex]p[/latex] that corresponds to the original point [latex](−2,2)[/latex] on the graph of [latex]f[/latex].
b. Sketch an accurate graph of the transformation [latex]y=q(x)=2g(x+0.5)−0.75[/latex]. Write at least one sentence to explain how you developed the graph of [latex]p[/latex], and identify the point on [latex]q[/latex] that corresponds to the original point [latex](1.5,1.5)[/latex] on the graph of [latex]g[/latex].
c. Is the function [latex]y=r(x)=\frac{1}{2}(−f(x−1)−4)[/latex] the same function as [latex]p[/latex] or different? Why? Explain in two different ways: discuss the algebraic similarities and differences between [latex]p[/latex] and [latex]r[/latex], and also discuss how each is a transformation of [latex]f[/latex].
d. Find a formula for a function [latex]y=s(x)[/latex] (in terms of g) that represents this transformation of [latex]g[/latex]: a horizontal shift of 1.25 units left, followed by a reflection across the [latex]x[/latex]-axis and a vertical stretch by a factor of 2.5 units, followed by a vertical shift of 1.75 units. Sketch an accurate, labeled graph of [latex]s[/latex] on the following axes along with the given parent function [latex]g[/latex].
Show Solution
a. [latex]y=p(x)=−\frac{1}{2}f(x−1)+2.[/latex]: This graph is Function [latex]f[/latex] that has been shifted right 1 unit, vertically compressed by a factor of 2, reflected across the horizontal axis and shifted up 2 units.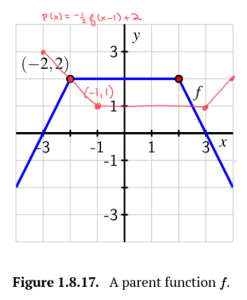
b. [latex]y=q(x)=2g(x+0.5)−0.75[/latex]: This graph is Function [latex]g[/latex] that has been shifted left 0.5 units, vertically stretched by a factor of 2 and shifted down 0.75 units.
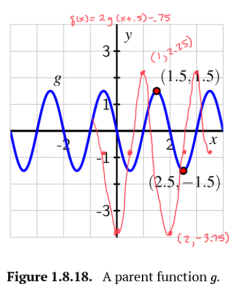c. No, they are not the same. It is not the same to reflect across the horizontal axis, shift down 4, then vertically compress by 2 as to first reflect, compress then shift up. The order of operations matter.
d. [latex]s(x)=-2.5g(x+1.25)+1.75[/latex]
1.8 Exercise 7
Consider the parent function [latex]y=f(x)=x[/latex].
a. Consider the linear function in point-slope form given by [latex]y=L(x)=−4(x−3)+5[/latex]. What is the slope of this line? What is the most obvious point that lies on the line?
b. How can the function [latex]L[/latex] given in (a) be viewed as a transformation of the parent function [latex]f[/latex]? Explain the roles of 3, −4, and 5, respectively.
c. Explain why any non-vertical line of the form [latex]P(x)=m(x−x_{0})+y_{0}[/latex] can be thought of as a transformation of the parent function f(x)=x. Specifically discuss the transformation(s) involved
d. Find a formula for the transformation of [latex]f(x)=x[/latex] that corresponds to a horizontal shift of 7 units left, a reflection across [latex]y=0[/latex] and vertical stretch of 3 units away from the [latex]x[/latex]-axis, and a vertical shift of −11 units.
Show Solution
a. [latex]m=-4[/latex]; [latex](-3,5)[/latex]
b. The Function [latex]f[/latex] has been shifted right 3 units, reflected across the vertical axis and vertically stretched by a factor of 4, and shifted up 5.
c. The Function [latex]f[/latex] has been shifted right [latex]x_{0}[/latex] units, vertically stretched/compressed by a factor of [latex]m[/latex], and shifted up [latex]y_{0}[/latex].
d. [latex]-3f(x+7)-11=-3(x+7)-11[/latex]