1.7 Inverse Functions
Activity 1.7.2
Recall Dolbear's function [latex]F=D(N)=40+14N[/latex] that converts the number, [latex]N[/latex], of snowy tree cricket chirps per minute to a corresponding Fahrenheit temperature. We have earlier established that the domain of [latex]D[/latex] is [latex][40,180][/latex] and the range of [latex]D[/latex] is [latex][50,85][/latex], as seen in Figure 1.2.3.
a. Solve the equation [latex]F=40+\frac{1}{4}N[/latex] for [latex]N[/latex] in terms of [latex]F[/latex]. Call the resulting function [latex]N=E(F)[/latex].
b. Explain in words the process or effect of the function [latex]N=E(F)[/latex]. What does it take as input? What does it generate as output?
c. Use the function [latex]E[/latex] that you found in (a.) to compute [latex]j(N)=E(D(N))[/latex]. Simplify your result as much as possible. Do likewise for [latex]k(F)=D(E(F))[/latex]. What do you notice about these two composite functions [latex]j[/latex] and [latex]k[/latex]?
d. Consider the equations [latex]F=40+14N[/latex] and [latex]N=4(F−40)[/latex]. Do these equations express different relationships between [latex]F[/latex] and [latex]N[/latex], or do they express the same relationship in two different ways? Explain.
Show Solution
a. [latex]F=40+\frac{1}{4}N[/latex]
[latex]F-40=\frac{1}{4}N[/latex]
[latex]4F-160=N[/latex]
[latex]N=E(F)=4F-160[/latex]
b. Number of chirps per minute as a function of the temperature in Fahrenheit.
Input: degrees Fahrenheit; Output: number of chirps.
c. [latex]j(N)=E(D(N))=E(40-\frac{1}{4}N)[/latex]
[latex]j(N)=4(40+\frac{1}{4}N)-160[/latex]
[latex]j(N)=N[/latex]
[latex]k(F)=D(E(F))=D(4F-160)[/latex]
[latex]k(N)=40+\frac{1}{4}(4F-160)[/latex]
[latex]k(N)=F[/latex]
d. It's the same relationship, just written in different ways. The input and output variables switched, but the relationship between N and F is still the same.
Activity 1.7.4 acde
During a major rainstorm, the rainfall at Gerald R. Ford Airport is measured on a frequent basis for a 10-hour period of time. The following function g models the rate, [latex]R[/latex], at which the rain falls (in cm/hr) on the time interval [latex]t=0[/latex] to [latex]t=10[/latex]:
[latex]R=g(t)=\frac{4}{t+2}+1[/latex]
a. Compute [latex]g(3)[/latex] and write a complete sentence to explain its meaning in the given context, including units.
b. Compute the average rate of change of [latex]g[/latex] on the time interval [latex][3,5][/latex] and write two careful complete sentences to explain the meaning of this value in the context of the problem, including units. Explicitly address what the value you compute tells you about how rain is falling over a certain time interval, and what you should expect as time goes on.
c. Plot the function [latex]y=g(t)[/latex] using a computational device. On the domain [latex][1,10][/latex], what is the corresponding range of [latex]g[/latex]? Why does the function [latex]g[/latex] have an inverse function?
d. Determine [latex]g^{−1}(95)[/latex] and write a complete sentence to explain its meaning in the given context.
e. According to the model [latex]g[/latex], is there ever a time during the storm that the rain falls at a rate of exactly 1 centimeter per hour? Why or why not? Provide an algebraic justification for your answer.
Show Solution
a. [latex]g(3)=\frac{4}{3+2}+1=\frac{9}{5}[/latex]
At three hours, the rain was falling at a rate of [latex]\frac{9}{5}[/latex] cm/hr.
b. SKIP
c. Domain: [latex][1,10][/latex], Range: [latex][\frac{7}{3},\frac{4}{3}][/latex]. Function [latex]g[/latex] has an inverse, because it passes the horizontal line test.
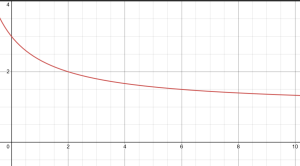
d. [latex]g^{-1}(\frac{9}{5})=3[/latex]. When the rain is falling at [latex]\frac{9}{5}[/latex] cm/hr, the time is 3 hours.
e. [latex]1=\frac{4}{t+2}+1[/latex]
[latex]0=\frac{4}{t+2}[/latex]
No, there is not a time when the rain is falling at 1 cm/hr. The fraction [latex]\frac{4}{t+2}[/latex] can never equal 0.
Recall that in Activity 1.6.3, we showed that Celsius temperature is a function of the number of chirps per minute from a snowy tree cricket according to the formula
[latex]C=H(N)=\frac{40}{9}+\frac{5}{36}N.[/latex]
a. What familiar type of function is [latex]H[/latex]? Why must [latex]H[/latex] have an inverse function?
b. Determine an algebraic formula for [latex]N=H−1(C)[/latex]. Clearly show your work and thinking.
c. What is the meaning of the statement [latex]72=H^{−1}(\frac{13}{09})[/latex]?
d. Determine the average rate of change of [latex]H[/latex] on the interval [latex][40,50][/latex]. Write a complete sentence to explain the meaning of the value you find, including units on the value. Explain clearly how this number describes how the temperature is changing.
e. Determine the average rate of change of [latex]H^{−1}[/latex] on the interval [latex][15,20][/latex]. Write a complete sentence to explain the meaning of the value you find, including units on the value. Explain clearly how this number describes how the number of chirps per minute is changing.
Show Solution
a. Function [latex]H[/latex] is a linear function. All (non-horiztonal) linear functions have inverses, because they pass the horizontal line test and are one to one.
b. [latex]N=H^{-1}(N)=\frac{36}{5}(C-\frac{40}{9})[/latex]. To find this inverse function, solve [latex]C=\frac{40}{9}+\frac{5}{36}N[/latex] for [latex]N[/latex].
c. This means that when the temperature is [latex]\frac{130}{9} \circ_{C}[/latex], there are 72 chirps.
d. SKIP
e. SKIP
