1.6 Composite Functions
Activity 1.6.2
Let functions [latex]p[/latex] and [latex]q[/latex] be given by the graphs in Figure 1.6.4 (which are each piecewise linear - that is, parts that look like straight lines are straight lines) and let [latex]f[/latex] and [latex]g[/latex] be given by Table 1.6.3.
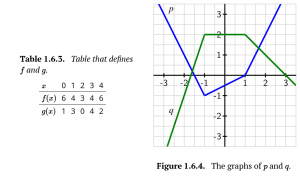
Compute each of the following quantities or explain why they are not defined.
a. [latex]p(q(0))[/latex]
b. [latex]q(p(0))[/latex]
c. [latex](p \circ p)(-1)[/latex]
d. [latex](f \circ g)(2)[/latex]
e. [latex](g\circ f)(3)[/latex]
f. [latex]g(f(0))[/latex]
g. For what value(s) of [latex]x[/latex] is [latex]f(g(x))=4[/latex]?
h. For what value(s) of [latex]x[/latex] is [latex]q(p(x))=1[/latex]?
Show Solution
a. [latex]p(q(0))=2[/latex]
b. [latex]q(p(0))=2[/latex]
c. [latex](p\circ p)(-1)=-1[/latex]
d. [latex](f\circ g)(2)=6[/latex]
e. [latex](g\circ f)(3)=2[/latex]
f. [latex]g(f(0))[/latex] is undefined, because [latex]f(0)=6[/latex], but there is no [latex]x=6[/latex] to find [latex]g(6)[/latex].
g. [latex]x=0, 1[/latex] when [latex]f(g(x))=4[/latex]
h. [latex]x=-2.5, 2[/latex] when [latex]q(p(x))=1[/latex]
Activity 1.6.3
Let [latex]F=D(N)=40+0.25N[/latex] be Dolbear's function that converts an input of number of chirps per minute to degrees Fahrenheit, and let [latex]C=G(F)=\frac{5}{9}(F-32)[/latex] be the function that converts an input of degrees Fahrenheit to an output of degrees Celsius.
a. Determine a formula for the new function [latex]H=(G\circ D)[/latex] that depends only on the variable [latex]N[/latex].
b. What is the meaning of the function you found in (a)?
c. How does a plot of the function [latex]H=(G\circ D)[/latex] compare to that of Dolbear's function? Sketch a plot of [latex]y=H(N)=(G\circ D)(N)[/latex] on the blank axes to the right of the plot of Dolbear's function, and discuss the similarities and differences between them. Be sure to label the vertical scale on your axes.
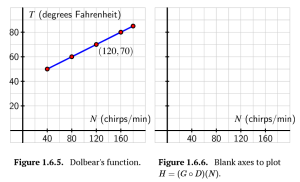
d. What is the domain of the function [latex]H=G\circ D[/latex]? What is the range?
Show Solution
a. [latex]H=(G\circ D)=\frac{5}{9}((40+.25N)-32)[/latex]
[latex]H(N)=\frac{40}{9}+\frac{5}{36}N[/latex]
b. Number of chirps gives the degrees in Celsius
c.
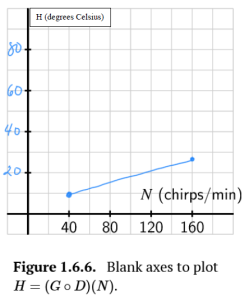
d. Domain: [latex][40, 160][/latex], Range: [latex][10, \frac{80}{3}][/latex]
1.6 Exercise 10
For each of the following functions, find two simpler functions [latex]f[/latex] and [latex]g[/latex] such that the given function can be written as the composite function [latex]g\circ f[/latex].
a. [latex]h(x)=(x^2+7)^3[/latex]
b. [latex]r(x)=\sqrt{5-x^3}[/latex]
c. [latex]m(x)=\frac{1}{x^4+2x^2+1}[/latex]
d. [latex]w(x)=2^{3-x^2}[/latex]
Show Solution
a. One possible solution: [latex]g(x)=x^3[/latex] and [latex]f(x)=x^2+7[/latex].
b. One possible solution: [latex]g(x)=\sqrt{x}[/latex] and [latex]f(x)=5-x^3[/latex]
c. One possible solution: [latex]g(x)=\frac{1}{x}[/latex] and [latex]f(x)=x^4+2x^2+1[/latex]
d. One possible solution: [latex]g(x)=2^x[/latex] and [latex]f(x)=3-x^2[/latex]
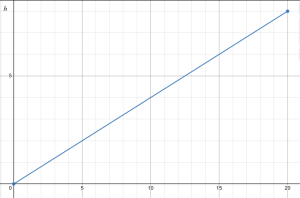
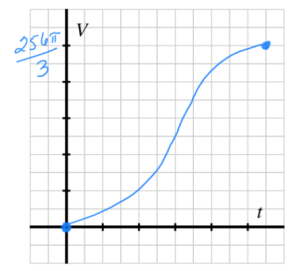
A spherical tank has radius 4 feet. The tank is initially empty and then begins to be filled in such a way that the height of the water rises at a constant rate of 0.4 feet per minute. Let [latex]V[/latex] be the volume of water in the tank at a given instant, and [latex]h[/latex] the depth of the water at the same instant; let [latex]t[/latex] denote the time elapsed in minutes since the tank started being filled.
a. Calculus can be used to show that the volume, [latex]V[/latex], is a function of the depth, [latex]h[/latex], of the water in the tank according to the function
[latex]V=f(h)=\frac{\pi}{3}h^2(12-h)[/latex]
What is the domain of this model? Why? What is the corresponding range?
b. We are given the fact that the tank is being filled in such a way that the height of the water rises at a constant rate of 0.4 feet per minute. Said differently, [latex]h[/latex] is a function of [latex]t[/latex] whose average rate of change is constant. What kind of function does this make [latex]h=p(t)[/latex]? Determine a formula for [latex]p(t)[/latex].
c. What are the domain and range of the function [latex]h=p(t)[/latex]? How is this tied to the dimensions of the tank?
d. In (a) we observed that [latex]V[/latex] is a function of [latex]h[/latex], and in (b) we found that [latex]h[/latex] is a function of [latex]t[/latex]. Use these two facts and function composition appropriately to write [latex]V[/latex] as a function of [latex]t[/latex]. Call the resulting function [latex]V=q(t)[/latex].
e. What are the domain and range of the function [latex]q[/latex]? Why?
f. On the provided axes, sketch accurate graphs of [latex]h=p(t)[/latex] and [latex]V=q(t)[/latex], labeling the vertical and horizontal scale on each graph appropriately. Make your graphs as precise as you can; use a computing device to assist as needed.
Why do each of the two graphs have their respective shapes? Write at least one sentence to explain each graph; refer explicitly to the shape of the tank and other information given in the problem.
Show Solution
a. Domain: [latex][0,8][/latex], Range: [latex][0, \frac{256\pi}{3}][/latex]
b. Linear; [latex]h=p(t)=0.4t[/latex]
c. Domain: [latex][0,20][/latex], Range: [latex][0,8][/latex]. The domain has to stop when the tank is full, at 20 minutes, when the max height is 8 ft.
d. [latex]V=\frac{\pi}{3}(.4t)^2(12-0.4t)[/latex]
e. Domain: [latex][0,20][/latex], Range: [latex][0,\frac{256\pi}{3}][/latex]. The time starts at 0 minutes and runs to 20 minutes, when the volume of the tank reaches its maximum of [latex]\frac{256\pi}{3}[/latex].
f.