1.5 Quadratic Functions

a. Changing the value of [latex]a[/latex] changes the overall shape of the graph. If [latex]a[/latex] is positive, then the quadratic function is facing up. Whereas if [latex]a[/latex] is negative, the graph faces down. Also, the larger the [latex]a[/latex] value is in absolute value the skinnier the graph is and the closer the [latex]a[/latex] value is closer to 0 the wider the graph is.

b. It is a bit harder to see how changing [latex]b[/latex] directly changes the graph. However, as we change [latex]b[/latex] it does change where the highest point of the graph is if the graph faces down and where the lowest point on the graph is if the graph faces up.

c. By changing the value of [latex]c[/latex] it impacts where the y-intercept is on the graph.

d. c is the parameter with the simplest effect because it tells us directly where the graph will cross the y-axis. The parameter [latex]b[/latex] has the most complicated effect. We can see that changing [latex]b[/latex] does impact the location of the highest or lower point of the graph. But the we cannot tell how the actual value of b directly impacts the graph itself.

e. We want to determine a formula for a quadratic equation [latex]q(x)[/latex] that passes through [latex](0,8)[/latex], [latex](1,12)[/latex], and [latex](2,12)[/latex]. We will put the equation into standard form [latex]q(x) = ax^2+bx+c[/latex]. Our goal is to determine the values of [latex]a[/latex], [latex]b[/latex], and [latex]c[/latex] in our equation.

Since the graph passes through [latex](0,8)[/latex] then we know that [latex]q(0) = 8[/latex]. So if we plug that into our equation we get [latex]a(0)^2 + b(0) + c = 8[/latex] which simplifies to [latex]c = 8[/latex]. So now we know that the value of [latex]c[/latex].

Next, we will plug in our two other given points [latex](1,12)[/latex] and [latex](2,12)[/latex] into [latex]q(x)[/latex] to get two separate equations to solve for [latex]a[/latex] and [latex]b[/latex]. First we will plug in [latex](1,12)[/latex] to get

\begin{align*}
12 & = a(1)^2 + b(1) + 8 \\
12 & = a + b + 8 \\
4 & = a+b \\
\end{align*}

Now we will plug in the second point [latex](2,12)[/latex]

\begin{align*}
12 & = a(2)^2+b(2)+8 \\
12 & = 4a+2b+8 \\
4 & = 4a+2b
\end{align*}

So we have two sets of equations [latex]a+b = 4[/latex] and [latex]4a+2b = 4[/latex]. We will solve the first equation for [latex]b[/latex] to get [latex]b = 4-a[/latex] and then we can substitute that into our second equation to solve for [latex]a[/latex].

\begin{align*}
4a+2b & = 4 \\
4a+2(4-a)& = 4 \\
4a+8-2a & = 4 \\
2a+8 & = 4 \\
2a & = -4 \\
a & = -2 \\
\end{align*}

Now that we have that [latex]a = -2[/latex] we can plug that back into equation 1: [latex]a+b=4[/latex] and solve for [latex]b[/latex] to get [latex]b = 6[/latex].

Thus, our equation is [latex]q(x) = -2x^2+6x+8[/latex].

a. We are given that the x-intercepts are [latex](-5,0)[/latex] and [latex](10,0)[/latex]. Based off this information we can write the quadratic in factored form: [latex]q(x) = a(x-10)(x+5)[/latex]. Now, we need to determine the value of [latex]a[/latex], the leading coefficient. Since the y-intercept is [latex](0,-1)[/latex] we can plug that into [latex]q(x)[/latex] to help us solve for [latex]a[/latex] to get:

\begin{align*}
-1 & = a(0-10)(0+5) \\
-1 & = a(-10)(5) \\
-1 & = -50a \\
a & = \frac{1}{50}
\end{align*}

Therefore our quadratic function is [latex]q(x) = \frac{1}{50}(x-10)(x+5)[/latex].

b. We know that the vertex is [latex](-3,-4)[/latex] and the quadratic opens upward. Using this information we can draw a picture. Based off the picture, we can see that the graph must pass through the x-axis in two different places meaning the graph has two x-intercepts.

c. From part (b) we know that the vertex is [latex](-3,-4)[/latex]. Using that information we can write our quadratic in vertex form to get: [latex]q(x) = a(x+3)^2-4[/latex]. Next, we know that [latex]q(-1) = -3[/latex] which is another point on the graph. We will plug in our point into [latex]q(x)[/latex]to help us solve for [latex]a[/latex].

\begin{align*}
-3 & = a(-1+3)^2-4 \\
-1 & = a(2)^2-4 \\
-1 & = 4a-4   \\
3 &  = 4a \\
a & = \frac{3}{4}
\end{align*}.

Thus, our quadratic function is [latex]q(x) = \frac{3}{4}(x+3)^2-4[/latex].

d. To determine the [latex]x[/latex]-intercepts, we start by setting [latex]q(x) = 0[/latex] and solving for [latex]x[/latex]:

\begin{align*}
0 & = -3(x+1)^2+9 \\
-9 & = -3(x+1)^2 \\
3 & = (x+1)^2 \\
\end{align*}

We then take the square root of both sides

\begin{align*}
\pm \sqrt{3} & = (x+1) \\
x & = -1 \pm \sqrt{3} \\
\end{align*}

So, the [latex]x[/latex]-intercepts are [latex]x = -1 + \sqrt{3}[/latex] and [latex]x = -1 - \sqrt{3}[/latex].

e.To determine the [latex]x[/latex]-intercepts we set [latex]w(x) = 0[/latex]. This gives us [latex]0 = -2x^2+10x-20[/latex]. This quadratic is not factorable so we will use the quadratic formula to find the [latex]x[/latex]-intercepts. Since [latex]a = -2[/latex], [latex]b = 10,[/latex] and [latex]c = -20[/latex] we get:

[latex]x = \frac{-10 \pm \sqrt{10^2-4(-2)(-20)}}{2(-2)} = \frac{-10 \pm \sqrt{100-160}}{-4} = \frac{-10 \pm \sqrt{-60}}{-4}[/latex].

The quadratic formula tells us there are imaginary roots because there is a negative under the square root. Hence, there are no [latex]x[/latex]-intercepts.

a. From chapter 1.5, we are given that the equation for modeling falling objects is given by [latex]s(t) = -16t^2+v_{0}+s_{0}[/latex] where [latex]v_{0}[/latex] is the initial velocity and [latex]s_{0}[/latex] is the initial height. With the information we are given our function is [latex]s(t) = -16t^2+41t+37[/latex].

b. Using Desmos:

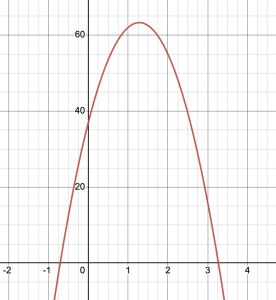
c. Using the graph we can estimate the water ballon takes [latex]3.25[/latex] seconds to land.

d. To determine the time it takes for the water ballon to land we want to find when the height of the function is zero that is when is [latex]s(t) = 0[/latex]. So, we have [latex]-16^2+41t+37 = 0[/latex]. This is not factorable so we will use the quadratic formula to solve. Using the quadratic formula we get:

[latex]t = \frac{-41 \pm \sqrt{(41)^2-4(-16)(37)}}{2(-16)}  = \frac{-41 \pm \sqrt{4049}}{-32} \approx -0.7072[/latex] and [latex]3.2697[/latex].

Since we cannot have negative time, so it takes [latex]3.2697[/latex] seconds for the water ballon to land. This is pretty close to our estimate from part c.

e. We want to determine the exact time the ballon reaches its highest point and the highest point of the ballon. We are essentially finding the vertex of the graph. To determine a vertex in standard form we use the formula:

[latex](\frac{-b}{2a},s(\frac{-b}{2sa}))[/latex].

Since [latex]a = -16[/latex] and [latex]b = 41[/latex], the [latex]t[/latex]-coordinate of the vertex is given by [latex]t = \frac{-(-41)}{2(16)} = \frac{41}{32} = 1.28125[/latex]. So, it takes [latex]1.2815[/latex] seconds for the water ballon to reach its maximum height.

So to determine the maximum height we will plug in [latex]t = 1.2815[/latex] into [latex]s(t)[/latex] to get [latex]s(1.2815) = -16(1.2815)^2+41(1.2815) +32 \approx 63.27[/latex]. Thus, the maximum height of the waterballon is [latex]63.27[/latex] feet.