5.2 Polynomials
Activity 5.2.2
By experimenting with coefficients in Desmos, find a formula for a polynomial function that has the stated properties, or explain why no such polynomial exists. (If you enter [latex]p(x)=a+bx+cx^2+dx^3+fx^4+gx^5[/latex] in Desmos, you'll get prompted to add sliders that make it easy to explore a degree 5 polynomial.)
a. A polynomial [latex]p[/latex] of degree 5 with exactly 3 real zeros, 4 turning points, and such that [latex]\lim_{x \to -\infty} p(x)=+\infty[/latex] and [latex]\lim_{x \to \infty} p(x)=-\infty[/latex].
b. A polynomial [latex]p[/latex] of degree 4 with exactly 4 real zeros, 3 turning points, and such that [latex]\lim_{x \to -\infty} p(x)=+\infty[/latex] and [latex]\lim_{x \to \infty} p(x)=-\infty[/latex].
c. A polynomial [latex]p[/latex] of degree 6 with exactly 2 real zeros, 3 turning points, and such that [latex]\lim_{x \to -\infty} p(x)=-\infty[/latex] and [latex]\lim_{x \to \infty} p(x)=-\infty[/latex].
d. A polynomial [latex]p[/latex] of degree 5 with exactly 5 real zeros, 3 turning points, and such that [latex]\lim_{x \to -\infty} p(x)=+\infty[/latex] and [latex]\lim_{x \to \infty} p(x)=-\infty[/latex].
Show Solution
a. One example is [latex]p(x)=1.3-.6x-10x^2+7.5x^3+1.4x^4-1.5x^5[/latex].
b. There is no polynomial that fits this description. With an even degree, the end behavior has to go in the same direction, either both to [latex]-\infty[/latex] or both to [latex]+\infty[/latex].
c. One example is [latex]p(x)=5.2-6.3x-9.4x^2+6.1x^3+1.5x^4+.3x^5-.7x^6[/latex].
d. Does not exist as you cannot have 5 distinct zeroes, with only 3 turning points.
Activity 5.2.3
Consider the polynomial function given by
[latex]p(x)=4692(x+1520)(x^2+10000)(x-3471)^2(x-9738)[/latex].
a. What is the degree of [latex]p[/latex]? How can you tell without fully expanding the factored form of the function?
b. What can you say about the sign of the factor [latex](x^2+10000)[/latex]?
c. What are the zeros of the polynomial [latex]p[/latex]?
d. Construct a sign chart for [latex]p[/latex] by using the zeros you identified in (c) and then analyzing the sign of each factor of [latex]p[/latex].
e. Without using a graphing utility, construct an approximate graph of [latex]p[/latex] that has the zeros of [latex]p[/latex] carefully labeled on the [latex]x[/latex]-axis.
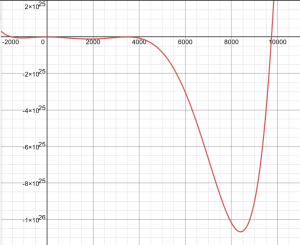
f. Use a graphing utility to check your earlier work. What is challenging or misleading when using technology to graph [latex]p[/latex].
Show Solution
a. The degree is 6. If you were going to expand this function, at some point, you'd multiple all of the [latex]x[/latex] terms together. Look at each factor and you'd have [latex]x\cdot x^2 \cdot x^2 \cdot x[/latex] which would end up as [latex]x^6[/latex].
b. It will always be positive, because any [latex]x[/latex] input will be squared, then adding 10000 keeps the term positive.
c. [latex]x=-1520, 3741[/latex], and [latex]9738[/latex] These were found by setting each factor equal to 0, and finding [latex]x[/latex].
d.

e. Answers will vary, but needs to be even shape, concave up, with zeroes at [latex]x=-1520, 3741, 9738[/latex], where [latex](3741,0)[/latex] is a double zero.
f. This graph is very challenging, because the values are so big.
Activity 5.2.4
For each of the following prompts, try to determine a formula for a polynomial that satisfies the given criteria. If no such polynomial exists, explain why.
a. A polynomial [latex]f[/latex] of degree 10 whose zeros are [latex]x=−12[/latex] (multiplicity 3), [latex]x=−9[/latex] (multiplicity 2), [latex]x=4[/latex] (multiplicity 4), and [latex]x=10[/latex] (multiplicity 1), and [latex]f[/latex] satisfies [latex]f(0)=21[/latex]. What can you say about the values of [latex]\lim_{x \to -\infty} f(x)[/latex] and [latex]\lim_{x \to \infty} f(x)[/latex].
b. A polynomial [latex]p[/latex] of degree 9 that satisfies [latex]p(0)=−2[/latex] and has the graph shown in Figure 5.2.14. Assume that all of the zeros of [latex]p[/latex] are shown in the figure.
c. A polynomial [latex]q[/latex] of degree 8 with 3 distinct real zeros (possibly of different multiplicities) such that [latex]q[/latex] has the sign chart in Figure 5.2.15 and satisfies [latex]q(0)=−10[/latex].
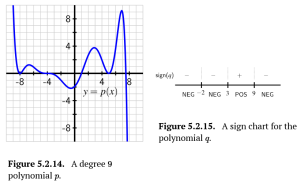
d. A polynomial [latex]q[/latex] of degree 9 with 3 distinct real zeros (possibly of different multiplicities) such that [latex]q[/latex] satisfies the sign chart in Figure 5.2.15 and satisfies [latex]q(0)=−10[/latex].
e. A polynomial [latex]p[/latex] of degree 11 that satisfies [latex]p(0)=−2[/latex] and [latex]p[/latex] has the graph shown in Figure 5.2.14. Assume that all of the zeros of [latex]p[/latex] are shown in the figure.
Show Solution
a. Start with satisfying the zeros and multiplicity:
[latex]f(x)=(x+12)^3(x+9)^2(x-4)^4(x-10)[/latex].
But a quick glance at this function will tell you that it does not satisfy [latex]f(0)=21[/latex].
So consider: [latex]f(x)=a(x+12)^3(x+9)^2(x-4)^4(x-10)[/latex] where we must find a value of [latex]a[/latex], such that [latex]f(0)=21[/latex].
Substitute and solve for [latex]a[/latex]:
[latex]21=a(0+12)^3(x+9)^2(0-4)^4(0-10)[/latex]. (Hint: use a calculator!).
[latex]a=-\frac{7}{119439360}[/latex], then write your final function:
[latex]f(x)=-\frac{7}{119439360}(x+12)^3(x+9)^2(x-4)^4(x-10)[/latex].
b. Similar to (a), start with satisfying the zeros and multiplicity: [latex]p(x)=a(x+8)^2(x+4)^3(x-1)(x-5)^2(x-7.5)[/latex]. Then use [latex]p(0)=-2[/latex] to find [latex]a[/latex].
Solve for [latex]a[/latex]:
[latex]-2=a(0+8)^2(x+4)^3(0-1)(0-5)^2(0-7.5)[/latex]. (Hint: use a calculator!).
[latex]a=\frac{1}{384000}[/latex], then write your final function:
[latex]p(x)=\frac{1}{384000}(x+8)^2(x+4)^3(x-1)(x-5)^2(x-7.5)[/latex]
c. First, addressing the zeroes and multiplicity, [latex]q(x)=(x+2)^6(x-3)(x-9)[/latex]. Then determine an [latex]a[/latex], such that [latex]q(0)=-10[/latex].
Solve for [latex]a[/latex]:
[latex]-10=a(0+2)^6(0-3)(0-9)[/latex]
[latex]a=\frac{-5}{864}[/latex]
Then, we have [latex]q(x)=\frac{-5}{864}(x+2)^6(x-3)(x-9)[/latex]. Finally, be sure to check that this function satisfies the given sign chart. For example, choose an [latex]x[/latex] that is less than -2, like -5, then make sure that when [latex]x=-5[/latex], the function is negative. Check that the function is negative between -2 and 3 as well, then positive when [latex]x[/latex] is between 3 and 9, and finally negative again when [latex]x[/latex] is greater than 9. The function [latex]q(x)=\frac{-5}{864}(x+2)^6(x-3)(x-9)[/latex] does indeed have this sign chart.
d. There is no polynomial that will satisfy this criteria. Note the degree of 9, then look at the sign chart. [latex]x=-2[/latex] must have an even multiplicity since the function is negative on both sides of -2. [latex]x=3[/latex] and [latex]x=9[/latex] must each be of odd multiplicity. The degree of this polynomial has to add up to 9; it is not possible to have multiplicities even, odd and odd add up to 9.
e. Start with [latex]p(x)=(x+8)^4(x+3)^3(x-1)(x-5)^2(x-7.5)[/latex]. Then use [latex]p(0)=-2[/latex] to find [latex]a.[/latex].
[latex]-2=a(0+8)^4(0+4)^3(0-1)(x-5)^2(0-7.5)[/latex] (Hint: use a calculator!)
[latex]a=\frac{-1}{24576000}[/latex]
So, [latex]p(x)=\frac{-1}{24576000}(x+8)^4(x+3)^3(x-1)(x-5)^2(x-7.5)[/latex].
5.2 Exercise 10
In each following question, find a formula for a polynomial with certain properties, generate a plot that demonstrates you’ve found a function with the given specifications, and write several sentences to explain your thinking.
a. A quadratic function [latex]q[/latex] has zeros at [latex]x=−7[/latex] and [latex]x=11[/latex] and its [latex]y[/latex]-value at its vertex is 42.
b. A polynomial [latex]r[/latex] of degree 4 has zeros at [latex]x=−3[/latex] and [latex]x=5[/latex], both of multiplicity 2, and the function has a [latex]y[/latex]-intercept at the point [latex](0,28)[/latex].
c. A polynomial [latex]f[/latex] has degree 11 and the following zeros: zeros of multiplicity 1 at [latex]x=−3[/latex] and [latex]x=5[/latex], zeros of multiplicity 2 at [latex]x=−2[/latex] and [latex]x=3[/latex], and a zero of multiplicity 3 at [latex]x=1[/latex]. In addition, [latex]\lim_{x \to \infty} f(x)=-\infty[/latex].
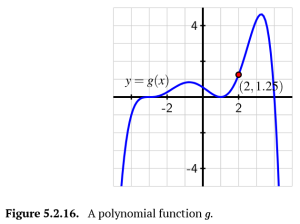
d. A polynomial [latex]g[/latex] has its graph given in Figure 5.2.16 below. Determine a possible formula for [latex]g(x)[/latex] where the polynomial you find has the lowest possible degree to match the graph. What is the degree of the function you find?
Show Solution
a. As this is a quadratic, start with [latex]q(x)=a(x+7)(x-11)[/latex]. Then solve for [latex]a[/latex] using that the [latex]y[/latex]-value at the vertex is 42. But what is the [latex]x[/latex]-value? Since this is quadratic, the vertex is halfway between the two zeroes. Halfway between -7 and 11 is 2, so the vertex of the function is [latex](2,42)[/latex].
[latex]42=a(2+7)(2-11)[/latex]
[latex]a=-\frac{14}{27}[/latex]
Then, [latex]q(x)=-\frac{14}{27}(x+7)(x-11)[/latex]
b. The zeroes and multiplicities give [latex]r(x)=a(x+3)^2(x-5)^2[/latex], then use [latex](0,28)[/latex] to find [latex]a[/latex].
[latex]28=a(0+3)^2(0-5)^2[/latex]
[latex]a=\frac{28}{225}[/latex]
Finally, [latex]r(x)=\frac{28}{225}(x+3)^2(x-5)^2[/latex].
c. This begins with [latex]f(x)=a(x+3)(x-5)(x+2)^2(x-3)^2(x-1)^3[/latex], but notice that the degree is not large enough. This is only degree 9. What we can do is add a factor that doesn't have any zeroes, like [latex]x^2+1[/latex]. This will give the function a degree of 11, but only have the stated zeroes.
[latex]f(x)=a(x+3)(x-5)(x+2)^2(x-3)^2(x-1)^3(x^2+1)[/latex]
Then we'll determine an [latex]a[/latex] such that [latex]\lim_{x \to \infty} f(x)=-\infty[/latex]. To satisfy this, [latex]a[/latex] should be any negative number, so one possible function is
[latex]f(x)=-(x+3)(x-5)(x+2)^2(x-3)^2(x-1)^3(x^2+1)[/latex].
d. To find a function [latex]g(x)[/latex], look at the overall shape of the graph, which is an even powered shape. Then determine its zeroes, which are [latex]x=-3[/latex] with odd multiplicity of at least 3, [latex]x=1[/latex] with even multiplicity, and [latex]x=4.[/latex].
Start the function: [latex]g(x)=a(x+3)^3(x-1)^2(x-4)[/latex]. Then use the vertical intercept of [latex](0,0.5)[/latex] to find [latex]a[/latex].
[latex]0.5=(0+3)^3(0-1)^2(0-4)[/latex]
[latex]a=-\frac{1}{216}[/latex]
So, [latex]g(x)=-\frac{1}{216}(x+3)^3(x-1)^2(x-4)[/latex].
