4.3 Inverses of trigonometric functions
Activity 4.3.2
Use the special points on the unit circle to determine the exact values of each of the following numerical expressions. Do some without using a computational device.
a.[latex]\arccos(\frac{1}{2})[/latex]
b.[latex]\arccos(\frac{\sqrt{2}}{2})[/latex]
c. [latex]\arccos(\frac{\sqrt{3}}{2})[/latex]
d. [latex]\arccos(-\frac{1}{2})[/latex]
e. [latex]\arccos(-\frac{\sqrt{2}}{2})[/latex]
f. [latex]\arccos(-\frac{\sqrt{3}}{2})[/latex]
g. [latex]\arccos(-1)[/latex]
h. [latex]\arccos(0)[/latex]
i. [latex]\cos(\arccos(-\frac{1}{2}))[/latex]
j. [latex]\arccos(\cos(\frac{7\pi}{6}))[/latex]
Show Solution
When we evaluate inverse trig functions we have to remember we are looking for an angle. In other words we are asking what angle gives us a cosine value of [latex]\frac{1}{2}[/latex]? That is, [latex]\arccos(\frac{1}{2})[/latex] is the same as [latex]\cos(\theta) = \frac{1}{2}[/latex]. So, now we will go to our unit circle.
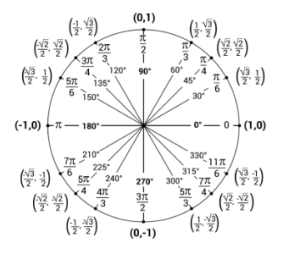
However, recall that the range of arccosine is from [latex][0,\pi][/latex] meaning when we evaluate our arccosine function our answer can only be an angle from [latex][0,\pi][/latex] which is the top half of the unit circle as seen below.
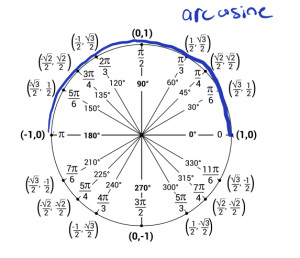
So, if we restrict ourselves to the top half we want to find where does cosine have a value of [latex]\frac{1}{2}[/latex]? Cosine is the [latex]x[/latex] coordinate of a point so cosine has a value of [latex]\frac{1}{2}[/latex] at [latex]\frac{\pi}{3}[/latex].
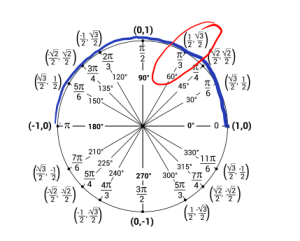
That is [latex]\cos(\frac{\pi}{3})[/latex]. Thus, [latex]\arccos(\frac{1}{2}) = \frac{\pi}{3}.[/latex].
b. We will use the same process as before. Now we are looking for the angle that gives us a cosine value of [latex]\frac{\sqrt{2}}{2}[/latex]. But, the angle needs to be in the interval [latex][0,\pi][/latex]. Using the unit circle we can see that happens at [latex]\frac{\pi}{4}[/latex].
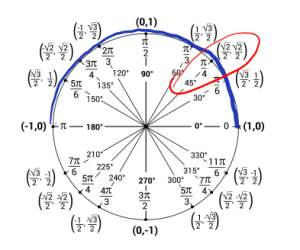
So, [latex]\arccos(\frac{\sqrt{2}}{2}) = \frac{\pi}{4}[/latex].
c. Now we are looking for the angle that gives us a cosine value of [latex]\frac{\sqrt{3}}{2}[/latex]. But, angle needs to be in the interval [latex][0,\pi][/latex]. Using the unit circle we can see that happens at [latex]\frac{\pi}{6}[/latex].
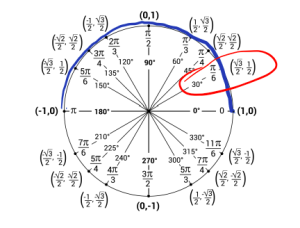
So, [latex]\arccos(\frac{\sqrt{3}}{2}) = \frac{\pi}{6}[/latex].
d. Now we are looking for what angle gives us a cosine value of [latex]-\frac{1}{2}[/latex] and angle needs to be in the interval [latex][0,\pi][/latex]. Since cosine is negative (as well as our [latex]x[/latex]-distance) we know to look in the second quadrant.
So using the circle we can see at [latex]\frac{2\pi}{3}[/latex] the cosine value is [latex]-\frac{1}{2}[/latex].
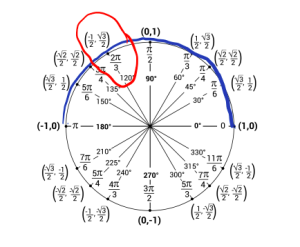
That is, [latex]cos(\frac{2\pi}{3}) = -\frac{1}{2}[/latex]. So, [latex]\arccos(-\frac{1}{2}) = \frac{2\pi}{3}[/latex].
e. Now we are looking for what angles gives us a cosine value of [latex]\frac{-\sqrt{2}}{2}[/latex] and the angle needs to be in the interval [latex][0,\pi][/latex]. Using the unit circle we can see that happens at [latex]\frac{3\pi}{4}[/latex].
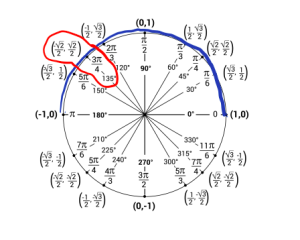
That is, [latex]\arccos(-\frac{\sqrt{2}}{2}) = \frac{3\pi}{4}[/latex].
f. Now we are looking for what angles gives us a cosine value of [latex]\frac{-\sqrt{3}}{2}[/latex] and the angle needs to be in the interval [latex][0,\pi][/latex]. Using the unit circle we can see that happens at [latex]\frac{5\pi}{6}[/latex].
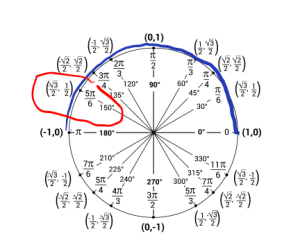
That is, [latex]\arccos(-\frac{\sqrt{3}}{2}) = \frac{5\pi}{6}[/latex].
g. Now we are looking for what angles gives us a cosine value [latex]-1[/latex] and angle needs to be in the interval [latex][0,\pi][/latex]. Using the unit circle we can see that happens at \pi.
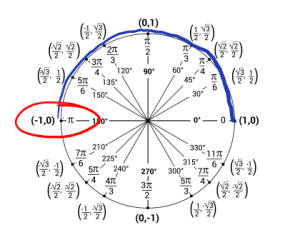
So, [latex]\arccos(-1) = \pi[/latex].
h. Now we are looking for what angles gives us a cosine value 0 and angle needs to be in the interval [0,\pi]. Using the unit circle we can see that happens at \frac{\pi}{2}.
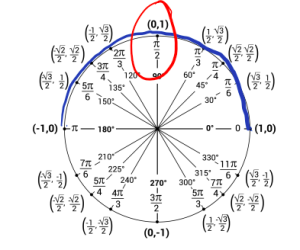
So, [latex]\arccos(0) = \frac{\pi}{2}[/latex].
i. With this problem we will start by evaluating the inside function that is [latex]\arccos(-\frac{1]{2})[/latex]. We want to find the angle that gives us a cosine value of [latex]\frac{-1}{2}[/latex] and the angle is in the interval from [[latex]0,\pi][/latex].

From our previous work we know this occurs at [latex]\frac{2\pi}{3}[/latex]. So, [latex]\arccos(-\frac{1}{2})) = \frac{2\pi}{3}[/latex]. Now going back into our original question and evaluating our inner function we have,
[latex]\cos(\arccos(-\frac{1}{2})) = \cos(\frac{2\pi}{3}) = -\frac{1}{2}[/latex].
j. We start by evaluating the inside function [latex]cos(\frac{7\pi}{6})[/latex]. Using the unit circle, [latex]cos(\frac{7\pi}{6}) = \frac{-\sqrt{3}}{2}[/latex]. So, we have
[latex]\arccos(\cos(\frac{7\pi}{6})) = \arccos(\frac{-\sqrt{3}}{2}) = \frac{5\pi}{6}[/latex] (from part f).
Activity 4.3.3
The goal of this activity is to understand key properties of the arcsine function in a way similar to our discussion of the arccosine function.
a. Using Definition 4.3.3, what are the domain and range of the arcsine function?
b. Determine the following values exactly: [latex]\arcsin(-1)[/latex], [latex]\arcsin(-\frac{-\sqrt{3}}{2}), \arcsin(0)[/latex], [latex]\arcsin(\frac{1}{2}),[/latex] [latex]\arcsin(\frac{\sqrt{3}}{2})[/latex].
c. On the axes provided in Figure 4.3.4, sketch a careful plot of the restricted sine function on the interval [latex][-\frac{\pi}{2}, \frac{\pi}{2}][/latex] along with its corresponding inverse, the arcsine function. Label at least three points on each curve so that each point on the sine graph corresponds to a point on the arcsine graph. In addition, sketch the line [latex]y=t[/latex] to demonstrate how the graphs are reflections of one another across the line.
d. True or false: [latex]\arcsin(\sin(5\pi)) = 5\pi[/latex]. Write a complete sentence to explain your reasoning.
Show Solution
a. By definition of inverses, we know that the domain of the sine function is the same as the range of its inverse the arcsine function. So, using definition 4.3.3. the range of the arcsine function is [latex][-\frac{\pi}{2}, \frac{\pi}{2}][/latex]. Similarly, the range of the sine function is the same as the domain of the arcsine function so the domain of the arcsine function is [latex][-1,1][/latex].
b. First we will find [latex]\arcsin(-1)[/latex]. When we evaluate inverse trig functions our answer is an angle. In other words we are asking what angle gives us a sine value of [latex]-1[/latex]. That is, [latex]\arcsin(-1)[/latex] is the same as [latex]cos(\theta) = -1[/latex]. So, now we go to the unit circle.

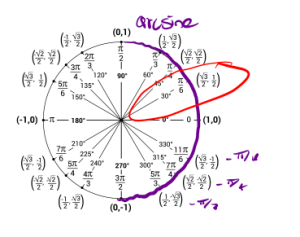
However, we will make note that from part a the range of arcsine is from [latex][-\frac{\pi}{2}, \frac{\pi}{2}][/latex] meaning when we evaluate our arcsine function our answer can only be an angle from [latex][-\frac{\pi}{2},\frac{\pi}{2}][/latex] which consists of the right half of the unit circle below:
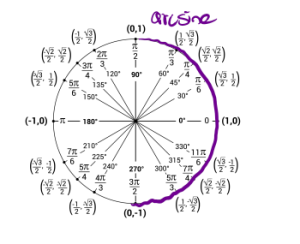
In the labeled picture I have labeled some key negative angles. Recall, that negative angles mean that we go in a clockwise direction.
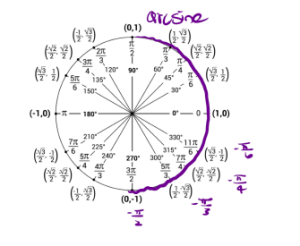
So using the unit circle, if we restrict ourselves on the interval [latex][-\frac{\pi}{2}, \frac{\pi}{2}][/latex], we want to find where does sine have a value of [latex]-1[/latex]. Sine is the [latex]y[/latex] coordinate of the point so sine has value of [latex]-1[/latex] at [latex]-\frac{\pi}{2}[/latex].
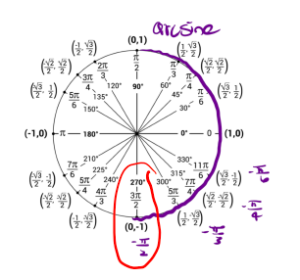
That is [latex]\sin(\frac{-\pi}{2}) = -1[/latex], so [latex]\arcsin(-1) = \frac{-\pi}{2}[/latex].
Now we will determine [latex]\arcsin(-\frac{\sqrt{2}}{2})[/latex]. That is, what angle gives us a sine value of [latex]-\frac{\sqrt{2}}{2}[/latex]. But, our angle must be in the interval [latex][-\frac{\pi}{2}, \frac{\pi}{2}][/latex]. So using the unit circle our angle is [latex]\frac{-\pi}{4}[/latex].
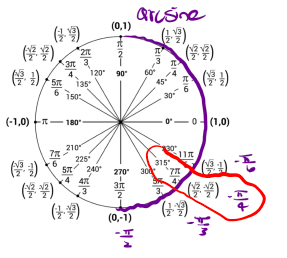
So, [latex]\arcsin(-\frac{\sqrt{2}}{2}) = -\frac{\pi}{4}[/latex].
Now we will determine [latex]arcsin(0) = 0[/latex]. That is, what angle gives us a sine value of [latex]0[/latex] and our angle must be in the interval [latex][-\frac{\pi}{2}, \frac{\pi}{2}][/latex]. So using the unit circle our angle is [latex]0[/latex].
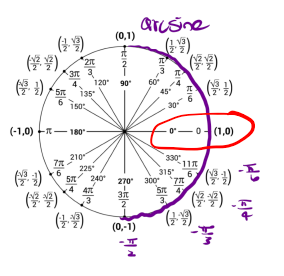
So, [latex]\arcsin(0) = 0[/latex].
Now we will determine [latex]\arcsin(\frac{1}{2}).[/latex] That is, what angle gives us a sine value of [latex]\frac{1}{2}[/latex]and our angle must be in the interval [latex][-\frac{\pi}{2}, \frac{\pi}{2}][/latex]. So using the unit circle our angle is [latex]\frac{\pi}{6}[/latex].
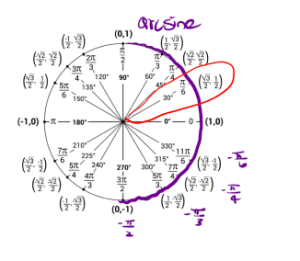
So, [latex]\arcsin(\frac{1}{2}) = \frac{\pi}{6}[/latex].
Finally, we will determine [latex]\arcsin(\frac{\sqrt{3}}{2})[/latex]. That is, what angle gives us a sine value of [latex]\frac{\sqrt{3}}{2}[/latex] and our angle must be in the interval [latex][-\frac{\pi}{2}, \frac{\pi}{2}][/latex]. So using the unit circle our angle is [latex]\frac{\pi}{3}[/latex].
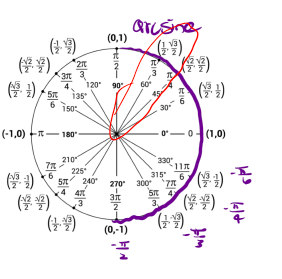
So, [latex]\arcsin(\frac{\sqrt{3}}{2}) = \frac{\pi}{3}[/latex].
c. Below is the graph of arcsine and sine on the interval [latex][-\frac{\pi}{2},\frac{\pi}{2}].[/latex]
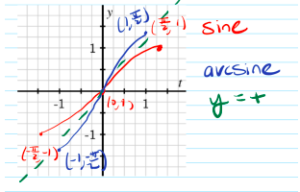
d. False. [latex]5\pi[/latex] is outside the range of the arcsine function of [latex][-\frac{\pi}{2}, \frac{\pi}{2}][/latex].
Exercise 5
Use the special points on the unit circle (see, for instance, Figure 2.3.1) to determine the exact values of each of the following numerical expressions. Do so without a computational device.
a.[latex]\arcsin(\frac{1}{2})[/latex]
b. [latex]\arctan(-1)[/latex]
c. [latex]\arcsin(-\frac{\sqrt{3}}{2})[/latex]
d. [latex]\arctan(-\frac{1}{\sqrt{3}})[/latex]
e. [latex]\arccos(\sin(\frac{\pi}{3}))[/latex]
f. [latex]\cos(\arcsin(-\frac{\sqrt{3}}{2})[/latex]
g. [latex]\tan(\arcsin(-\frac{\sqrt{2}}{2}))[/latex]
h. [latex]\arctan(\sin(\frac{\pi}{2}))[/latex]
i. [latex]\sin(\arcsin(-\frac{1}{2}))[/latex]
j. [latex]\arctan(\tan(\frac{7\pi}{4})[/latex]
Show Solution
a. We are looking for what angle gives us a sine value of [latex]\frac{1}{2}[/latex]. Recall, that the range of arcsine is [latex][-\frac{\pi}{2},\frac{\pi}{2}][/latex]. Using the unit circlewe have that [latex]\arcsin(\frac{1}{2}) = \frac{\pi}{6}[/latex].
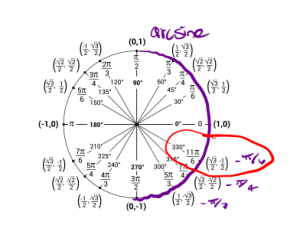
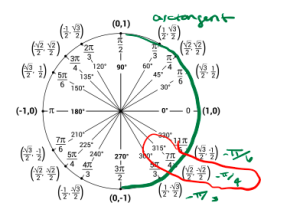
b. We are looking for an angle that gives us a tangent value of [latex]-1[/latex]. Also, we must keep in mind the range of arctangent is [latex](-\frac{\pi}{2},\frac{\pi}{2})[/latex]. Using the unit circle we have that [latex]\arctan(-1) = \frac{-\pi}{4}[/latex].
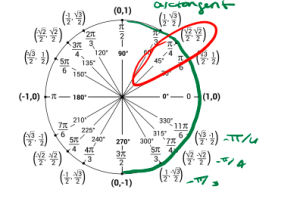
c. We are looking for what angle gives us a sine value of [latex]\frac{-\sqrt{3}}{2}[/latex]. Also, we must keep in mind the range of arcsine is [latex][-\frac{\pi}{2},\frac{\pi}{2}][/latex]. Using the unit circle we have that [latex]\arcsin(-\frac{\sqrt{3}}{2}) = -\frac{\pi}{3}[/latex].
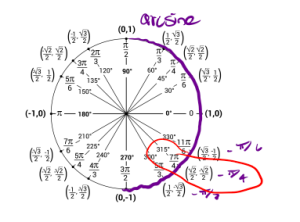
d. We are looking for an angle that gives us a tangent value of [latex]-\sqrt{1}{\sqrt{3}}[/latex]. Also, we must keep in mind the range of arctangent is [latex](-\frac{\pi}{2},\frac{\pi}{2}).[/latex] Using the unit circle we have [latex]\arctan(-\frac{1}{\sqrt{3}} = \frac{-\pi}{6}[/latex].
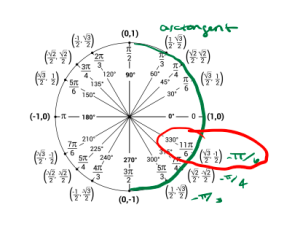
e. We start by evaluating the inside function first: [latex]sin(\frac{\pi}{3}) = \frac{\sqrt{3}}{2}[/latex]. So now we have,
[latex]\arccos(\frac{\sqrt{3}}{2}[/latex]). So now we are looking for what angle gives us a cosine value of [latex]\frac{\sqrt{3}}{2}[/latex] and we need to remember that the range of arccosine is [latex][0,\pi][/latex]. Using the unit circle we get that [latex]\arccos(\frac{\sqrt{3}}{2}) = \frac{\pi}{6}[/latex].
So, [latex]\arccos(\sin(\frac{\pi}{3})) = \arccos(\frac{\sqrt{3}}{2})= \frac{\pi}{6}[/latex].
f. We start by evaluating the inside function first. We want to determine [latex]\arcsin(-\frac{\sqrt{3}}{2}) = \frac{-\pi}{3}[/latex] from part c. So, we have
[latex]\cos(\arcsin(-\frac{-\sqrt{3}}{2})) = \cos(\frac{-\pi}{3}) = \frac{1}{2}[/latex].
g. We start by evaluating the inside function first, [latex]\arcsin(-\frac{\sqrt{2}}{2})[/latex]. We want to find the angle that gives us a sine value of [latex]\frac{-\sqrt{2}}{2}[/latex] and we must keep in mind the range of arcsine which is [latex][-\frac{\pi}{2},\frac{\pi}{2}][/latex]. So using the unit circle we have that [latex]\arcsin(\frac{-\sqrt{2}}{2})) = \frac{-\pi}{4}[/latex].
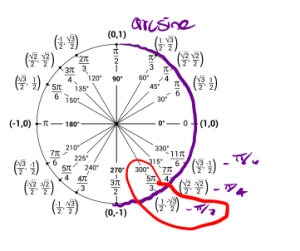
So, we have
[latex]\tan(\arcsin(-\frac{\sqrt{2}}{2})) = \tan(\frac{-\pi}{4}) = -1[/latex].
h. We first evaluate the inside function: [latex]\sin(\frac{\pi}{2}) = 1[/latex]. Now we want to find [latex]\arctan(1)[/latex]. We are looking for an angle that gives us a tangent value of [latex]1[/latex]. Also, we must keep in mind the range of arctangent is [latex](-\frac{\pi}{2},\frac{\pi}{2})[/latex]. Using the unit circle we have that [latex]\arctan(1) = \frac{\pi}{4}[/latex].
Therefore, [latex]\arctan(\sin(\frac{\pi}{2})) = \arctan(1) = \frac{\pi}{4}[/latex].
i. We evaluate the inside function first: [latex]\arcsin(\frac{-1}{2})[/latex]. We are looking for what angle gives us a sine value of [latex]\frac{-1}{2}[/latex] and we must keep in mind that the range of arcsine is [latex][-\frac{\pi}{2},\frac{\pi}{2}][/latex]. Using the unit circle we have that [latex]\arcsin(\frac{-1}{2}) = \frac{-\pi}{6}[/latex].
So now we have, [latex]\sin(\arcsin(\frac{-1}{2})) = \sin(\frac{-\pi}{6}) = \frac{-1}{2}[/latex].
j. We evaluate the inside function first: [latex]\tan(\frac{7\pi}{4}) = -1[/latex]. Now what we want to find is [latex]\arctan(-1)[/latex] which from part b we know [latex]\arctan(-1) = \frac{-\pi}{4}[/latex]. So,
[latex]\arctan(\tan(\frac{7\pi}{4})) = \arctan(-1) = \frac{-\pi}{4}[/latex].
Exercise 7
Let’s consider the composite function [latex]h(x) = \cos(\arcsin(x))[/latex]. This function makes sense to consider since the arcsine function produces an angle, at which cosine function can be evaluated. In the questions that follow, we investigate how to express [latex]h[/latex] without using trigonometric functions at all.
a. What is the domain of [latex]h[/latex]? The range of [latex]h[/latex]?
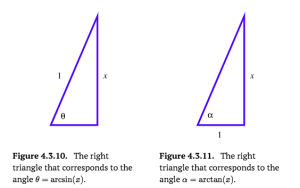
b. Since the arcsine function produces an angle, let’s say [latex]\theta = \arcsin(x[/latex]) so that \theta is the angle whose sine is [latex]x[/latex]. By definition, we can picture [latex]\theta[/latex] as an angle in a right triangle with hypotenuse [latex]1[/latex] and vertical leg of length [latex]x[/latex], as shown in Figure 4.3.10. Use the Pythagorean Theorem to determine the length of the horizontal leg as a function of [latex]x[/latex].
c.What is the value of [latex]\cos(\theta)[/latex] as a function of x? What have we shown about [latex]h(x) = \cos(\arcsin(x))[/latex]?
d. How about the function [latex]p(x) = \cos(\arctan(x))[/latex]? How can you reason similarly to write [latex]p[/latex] in a way that doesn’t involve trigonometric functions at all? (Hint: let [latex]\alpha = \arctan(x)[/latex] and consider the right triangle in Figure 4.3.11.)
Show Solution
a. Domain: [latex][-1,1][/latex], Range: [latex][0,1][/latex]
b. We will denote the horizontal leg of the right triangle as [latex]y[/latex]. So using the Pythagorean theorem we have [latex]x^2 + y^2 = 1[/latex]. Solving for [latex]y[/latex] gives [latex]\sqrt{1-x^2}[/latex]. So the length of the horizontal leg as a function of [latex]x[/latex] is [latex]\sqrt{1-x^2}[/latex].
c. Using the definition that [latex]\cos(\theta) = \frac{adj}{hyp}, \cos(\theta) = \frac{\sqrt{1-x^2}}{1} = \sqrt{1-x^2}[/latex]. Thus, [latex]\cos(\arcsin(x)) = \cos(\theta) = \sqrt{1-x^2}[/latex]. So, [latex]\cos(\arcsin(x)) = \sqrt{1-x^2}[/latex].
d. Let [latex]\alpha = \arctan(x)[/latex]. Using the triangle drawn in Figure 4.3.11, we will first solve for the length of the hypotenuse in terms of [latex]x[/latex] using the pythagorean theorem. We will label the hypotenuse [latex]c[/latex]. So we have [latex]1^2 + x^2 = c^2[/latex]. Solving for c gives [latex]c = \sqrt{1 + x^2}[/latex]. So, the length of the hypotenuse is [latex]\sqrt{1+x^2}[/latex]. So using the right triangle definition of cosine we have [latex]\cos(\alpha) = \frac{1}{\sqrt{1-x^2}}[/latex]. Thus, [latex]\cos(\arctan(x)) = \cos(\alpha) = \frac{1}{\sqrt{1-x^2}}[/latex].
