4.2 The Tangent Functions

Sherri Spriggs; Marcela Gutierrez

4.2 The Tangent Functions

Activity 4.2.2

The top of a

22

ft foot tower is to be anchored by four cables that each make an angle of

{32.5}^{\circ}

with the ground. How long do the cables have to be and how far from the base of the tower must they be anchored?

Show Solution

First, we will draw a picture of the situation below. We will start by solving for the length of the cables (c) Using the perspective that $\sin (θ) = \frac{o p p}{h y p}$ we have that

$\sin (32.5) = \frac{225}{c}$

We then multiply c on both sides to get $c \cdot \sin (32.5) = 225.$ Dividing both sides by $\sin (32.5)$ yields $c = \frac{225}{\sin (32.5)} \approx 418. 76$ .

Thus, the length of the cable should be about $418.76$ feet.

Now we will determine how far from the base of the tower the cables should be which is b in the figure. Using the perspective that $\tan (θ) = \frac{o p p}{h y p}$ we have that

$\tan (θ) = \frac{225}{b}$ .

We then multiply both sides of the equation by $b$ to get $b \cdot \tan (32.5) = 225$ . Dividing both sides by $\tan (32.5)$ yields $b = \frac{225}{\tan (32.5)} \approx 353.17$ .

Thus, the cables should be about $353.17$ feet away from the base of the tower.

Examples

Surveyors are trying to determine the height of a hill relative to sea level. First they choose a point to take an initial measurement with a sextant that shows the angle of elevation from the ground to the peak of the hill is $19^{\circ}$ . Next they move $1000$ feet closer to the hill, staying at the same elevation relative to sea level, and find that the angle of elevation has increased to $25^{\circ}$ , as pictured in Figure 4.2.11. We let $h$ represent the height of the hill relative to the two measurements, and $x$ represent the distance from the second measurement location to the “center” of the hill that lies directly under the peak

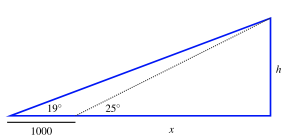
Figure 4.2.11 The Surveyors Initial Measurements

Use the right triangle with the $25^{\circ}$ angle, find an equation that relates x and h.
Using the right triangle with the $19^{\circ}$ angle, find a second equation that relates $x$ and $h$ .
Our work in (a) and (b) results in a system of two equations in the two unknowns $x$ and $h$ . Solve each of the two equations for $h$ and then substitute appropriately in order to find a single equation in the variable $x$ .
Solve the equation from (c) to find the exact value of $x$ and determine an approximately value accurate to $3$ decimal places.
Use your preceding work to solve for $h$ exactly, plus determine an estimate accurate to $3$ decimal places.
If the surveyors’ initial measurements were taken from an elevation of $78$ feet above seat level, how high above sea level is the peak of the hill?

Show Solution

a. Using the perspective that $\tan (θ) = \frac{o p p}{h y p}$ , in the triangle with the $25^{\circ}$ angle, we have that

$\tan (25^{\circ}) = \frac{h}{x}$ .

b. Again, we can use the fact that $\tan (θ) = \frac{o p p}{h y p}$ to get

$\tan (19^{\circ}) = \frac{h}{x + 1000}$ .

c. We will first solve the equation part a for h. We will start by multiplying the denominator on both sides by $x$ .

$\begin{aligned} \tan (25^{\circ}) * & = \frac{h}{x} \\ h & = x \tan (25^{\circ}) \end{aligned}$

Now we will solve the equation from part b by clearing the denominator.

$\begin{aligned} \tan (19^{\circ}) * & = \frac{h}{x + 1000} \\ h & = (x + 1000) \tan (19^{\circ}) \end{aligned}$

Now since both equations are equal to $h$ , they must be equal to each-other. We will now set both equations equal to one another to get

$(x + 1000) \tan (19^{\circ}) = x \tan (25^{\circ})$ .

d. We will solve the equation from part c for $x$ . We will start by distributing on the left hand side and then moving all the $x$ terms on one side.

$\begin{aligned} (x + 1000) \tan (19^{\circ}) & = x \tan (25^{\circ}) \\ x \tan (19^{\circ}) + 1000 \tan (19^{\circ}) & = x \tan (25^{\circ}) \\ x \tan (25^{\circ}) - x \tan (19^{\circ}) & = 1000 t a n (19^{\circ}) \\ x (\tan (25^{\circ}) - \tan (19^{\circ})) & = 1000 t a n (19^{\circ}) \\ x & = \frac{1000 \tan (19^{\circ})}{\tan (25^{\circ}) - \tan (19^{\circ})} \\ x & \approx 2822.819 \end{aligned}$

e. From part d, we have that $x = \frac{1000 \tan (19^{\circ})}{\tan (25^{\circ}) - \tan (19^{\circ})}$ . We will plug that into one of our equations from part c when we solved for $h$ . We have that $h = x \tan (25^{\circ}) = \frac{\tan (25^{\circ}) 1000 \tan (19^{\circ})}{\tan (25^{\circ}) - \tan (19^{\circ})} \approx 1316.302$ .

f. We add the elevation to the height of the hill to get $78 + 1316.302 = 1394.302$ feet. The peak of the hill 1394.302 feet above sea level.
<details

License

Icon for the Creative Commons Attribution-ShareAlike 4.0 International License

License

Share This Book