3.1 Exponential Growth and Decay
Activity 3.1.2
In Desmos, define the function [latex]g(t) = ab^t[/latex]and create slides for both [latex]a[/latex] and [latex]b[/latex] when prompted. Click on the slides to set the minimum value for each to 0.1 and the maximum value to 10. Note that for [latex]g[/latex] to be an exponential function, we require [latex]b \ne 1,[/latex] even though the slider for [latex]b[/latex] will allow this value.
a. What is the domain of [latex]g(t) = ab^t[/latex]
b. What is the range of [latex]g(t) = ab^t?[/latex]
c. What is the y-intercept of [latex]g(t) = ab^t[/latex]?
d. How does changing the value of [latex]b[/latex] affect the shape and behavior of the graph of [latex]g(t) = ab^t[/latex]Write several sentences to explain.
e. For what values of the growth factor [latex]b[/latex] is the corresponding growth rate positive? For which [latex]b[/latex]-values is the growth rate negative?
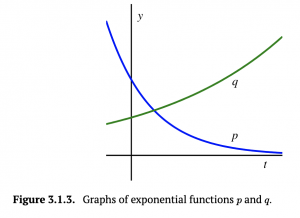
f. Consider the graphs of the exponential functions [latex]p[/latex] and [latex]q[/latex] provided in Figure 3.1.3 below. If [latex]p(t) = ab^t[/latex] and [latex]q(t) = cd^t[/latex], what can you say about the values of [latex]a,b,c[/latex] and [latex]d[/latex] (beyond the fact that all are positive and [latex]b \ne 1[/latex]and [latex]d \ne 1)[/latex]? For instance, can you say a certain value is larger than another? Or that one of the values is less than 1.
Show Solution
a. The domain of [latex]g(t)[/latex]is [latex](-\infty,\infty).[/latex]
b. The range of [latex]g(t)[/latex]is [latex](0,\infty).[/latex]
c. The y-intercept of [latex]g(t)[/latex]is [latex](0,a).[/latex]
d. If [latex]b > 1[/latex], then the shape of the function is increasing and if [latex]b<1[/latex] then the shape of the function is decreasing. Larger values of b make the graph grow at a faster rate. Similarly, b values closer to 0 make the graph decrease at a faster rate. e. We know that [latex]b = 1 r[/latex] so [latex]r = b-1.[/latex] If b > 1, then the growth rate [latex]r[/latex] is positive. Similarly, if [latex]b < 1[/latex], then the growth rate r is negative. f. From the graph, we can see that [latex]q[/latex] is an increasing graph and [latex]p[/latex] is a decreasing graph. That means that the value of 'b' in the [latex]q(t)[/latex] graph is less than 1. We also know from part c that the [latex]y-[/latex] intercept of [latex]p(t)[/latex] is (0,a) and the y-intercept of [latex]q(t)[/latex] is [latex](0,c)[/latex]. Visually, we can see that the y-intercept of [latex]p(t)[/latex] is greater than [latex]q(t0[/latex]. Hence, [latex]a > c[/latex].
Activity 3.1.3
The value of an automobile is depreciating. When the car is [latex]3[/latex] years old, its value is [latex]$12500[/latex]; when the car is [latex]7[/latex] years old, its value is [latex]$6500.[/latex]
a. Suppose that the car's value [latex]t[/latex] years after its purchase is given by the function [latex]V(t)[/latex] and [latex]V[/latex] is exponential with form [latex]V(t)=ab^t[/latex], what are the exact values of [latex]a[/latex] and [latex]b[/latex]?
b. Using the exponential model determined in (a), determine the purchase value of the car and estimate when the car will be worth less than [latex]$1000[/latex].
c. Suppose instead that the car's value is modeled by a linear function [latex]L[/latex] and satisfies the values stated at the outset of this activity. Find a formula for [latex]L(t)[/latex] and determine both the purchase value of the car and when the car will be worth [latex]$1000[/latex].
d. Which model do you think is more realistic? Why?
Show Solution
a. We know that when the car is [latex]3[/latex] years old the value is [latex]$12500[/latex] and when the car is is [latex]7[/latex] years old the value is [latex]$6500[/latex]. This gives us two data points of the equation [latex]V(t) = ab^t (3,12500)[/latex] and [latex](7,6500)[/latex]. We will plug in these two points into [latex]V(t)[/latex] to solve for [latex]a[/latex] and [latex]b[/latex]. First, we plug in [latex]t = 3[/latex] to get,
[latex]ab^3 = 12500[/latex] (equation 1)
and then plug in [latex]t = 7[/latex] to get,
[latex]ab^7 = 6500[/latex] (equation 2)
Because we know that the quotient of outputs of an exponential function corresponding to equally spaced inputs is constant we can consider the quotient [latex]\frac{6500}{12500}[/latex]. Form our work above we end up with the following
[latex]\frac{6500}{12500} = \frac{ab^7}{ab^3}[/latex]
Now we will simplify this expression to first solve for [latex]b[/latex]:
\begin{align*}
\frac{6500}{12500} & = \frac{ab^7}{ab^3} \\
\frac{6500}{12500} & = \frac{b^7}{b^3} \\
\frac{6500}{12500} & = b^4 \\
\frac{65}{125} & = b^4 \\
b & = (\frac{65}{125})^{\frac{1}{4}} \\
\end{align*}
Now we substitute [latex]b = (\frac{65}{125})^{\frac{1}{4}}[/latex] into equation (1) we get [latex]a((\frac{65}{125})^{\frac{1}{4}})^3 = 12500[/latex]. We then solve for [latex]a[/latex] to get
[latex]a = \frac{12500}{((\frac{65}{125})^{\frac{1}{4}})^3} = \frac{12500}{(\frac{65}{125})^{\frac{3}{4}}}[/latex].
So our equation is [latex]V(t) = \frac{12500}{(\frac{65}{125})^{\frac{3}{4}}}((\frac{65}{125})^{\frac{1}{4}})^t[/latex]
b. Using our equation from part a, we want to determine the purchase value of the car. This is when [latex]t = 0[/latex]. So we plug in [latex]t = 0[/latex] into [latex]V(t)[/latex] to get
[latex]V(0) = \frac{12500}{(\frac{65}{125})^{\frac{3}{4}}}((\frac{65}{125})^{\frac{1}{4}})^0 = \frac{12500}{(\frac{65}{125})^{\frac{3}{4}}} = \approx 20413.03[/latex].
We will graph [latex]V(t)[/latex] in desmos to determine when the car will be worth less than [latex]$1000[/latex].
Based off the graph, the car will be worth less than [latex]$1000[/latex] in [latex]18.3[/latex] years.
c. First we will determine a linear model L(t). We will write our model in point slope form. Given two points on the model [latex](3,12500)[/latex] and [latex](7,6500)[/latex], we will first determine the slope:
[latex]m = \frac{6500-12500}{7-3} = \frac{-6000}{4} = -1500[/latex].
Using point slope form with [latex]m = -1500[/latex] and point [latex](7,6500)[/latex] our model is [latex]y - 6500 = -1500 (t-7)[/latex]. We can now write this in slope intercept form by solving for [latex]y[/latex]. So we have,
\begin{align*}
y - 6500 & = -1500(t-7) \\
y - 6500 & = -1500t + 10500 \\
y & = -1500t + 17000 \\
\end{align*}
So our linear model [latex]L(t) = -1500t+17000[/latex].
Now, we want to determine the purchase value of the car this is the same as the vertical intercept (when [latex]t = 0[/latex]) which in the case is [latex]$17000[/latex].
Finally, we want to determine when the car will be less than [latex]$1000[/latex]. We set our equation [latex]L(t) = 1000[/latex] and solve for [latex]t[/latex].
\begin{align*}
1000 & = -1500t+17000 \\
-16000 & = -1500t \\
t & \approx 10.66 \\
\end{align*}
In about [latex]10.66[/latex] years the car will be less than [latex]$1000[/latex].
d. The exponential model is more realistic. It does not make sense that the car will depreciate by the same amount each year. As time goes on the car will be losing its worth quicker as new cars are made which is demonstrated by the exponential model.
