1.4 Linear Functions
Activity 1.4.2
Find an equation for the line that is determined by the following conditions; write your answer in point-slope form wherever possible.
- The line with slope [latex]\frac{3}{7}[/latex] that passes through [latex](-11,-17)[/latex].
- The line passing through the points [latex](-2,5)[/latex] and [latex](3,-1)[/latex].
- The line passing through [latex](4,9)[/latex] and that is parallel to the line [latex]2x-3y=5[/latex].
- Explain why the function [latex]f[/latex] given by Table 1.4.5 appears to be linear and find a formula for [latex]f(x)[/latex].
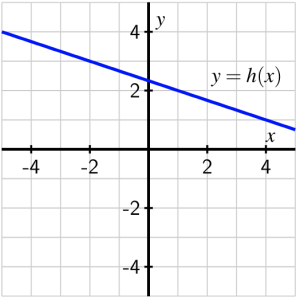
- Find a formula for the linear function shown in Figure 1.4.6.
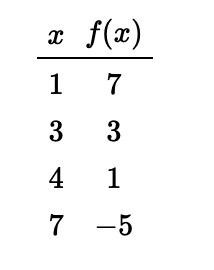
Show Solution
a. We know the slope is [latex]m=\frac{3}{7}[/latex] and the line passes through the point [latex](-11,-17)[/latex]. We then write the equation of the line in point slope form [latex]y = y_{0}+m(x-x_{0})[/latex] to get
[latex]y = -17+\frac{3}{7}(x+11)[/latex].
b. First, we start by finding the slope using the slope formula: [latex]m = \frac{-1-5}{3+2} = \frac{-6}{5}[/latex]
Now we can use either of the two points given to write the line in point slope form. We will use the point [latex](-2,5)[/latex] to get the following equation of a line:
[latex]y=5-\frac{6}{5}(x+2)[/latex].
c. We want to find the equation of a line that is parallel to [latex]2x-3y=5[/latex], which means our equation of the line must have the same slope as the line given. We first find the slope of [latex]2x-3y=5[/latex]. We will put the equation of the line into slope intercept form [latex]y = mx+b[/latex]. to determine the slope. Start by solving for [latex]y[/latex] to get [latex]y = \frac{2}{3}x-\frac{5}{3}[/latex]. The slope is the coefficient in front of [latex]x[/latex] so the slope of the line is [latex]m = \frac{2}{3}[/latex]. Thus, our equation of our line has the same slope of [latex]m = \frac{2}{3}[/latex] and passes through the point [latex](4,9)[/latex]. Using this information we can now write the equation of the line as follows:
[latex][latex]y=9+\frac{2}{3}(x-4)[/latex].[/latex]
d. In order for a function to be linear it must have constant slope. So, we will choose two sets of two different points in the table and calculate the slope for each. First, we will find the slope using the points [latex](1,7)[/latex] and [latex](4,1)[/latex]to get [latex]m = \frac{1-7}{4-1}=\frac{-6}{3} = -2[/latex]. Now we will find the slope using two different points in the table: [latex](4,1)[/latex] and [latex](7,-5)[/latex]to get [latex]m= \frac{-5-1}{7-4} = \frac{-6}{3}=-2[/latex].
Thus, regardless of the points we chose the rate of change was constant so the table represents a linear function.
e. To find the equation of a line in point slope form we need to have the slope and a point on the line. We will first calculate the slope using two points on the line: [latex](-2,3)[/latex] and [latex](4,1)[/latex]. The slope is [latex]m = \frac{1-3}{4-(-2)} = \frac{-2}{6} = \frac{-1}{3}[/latex]. Now we can use either of the two points to write our equation of the line. We will use the point [latex](4,1)[/latex] to get
[latex]y=1-\frac{1}{3}(x-4)[/latex].
Activity 1.4.3
The summit of Africa's largest peak, Mt. Kilimanjaro, has two main ice fields and a glacier at its peak. Geologists measured the ice cover in the year 2000 ([latex]t=0[/latex]) to be approximately [latex]1951 m^2[/latex]; in the year 2007, the ice cover measured [latex]1555 m^2[/latex].
-
- Suppose that the amount of ice cover at the peak of Mt. Kilimanjaro is changing at a constant average rate from year to year. Find a linear model [latex]A = f(t)[/latex] whose output is the area, [latex]A[/latex], in square meters in year [latex]t[/latex] (where [latex]t[/latex] is measured in the number of years after 2000).
- What do the slope and [latex]A[/latex]-intercept mean in the model you found in (a)? In particular, what are the units on the slope?
- Compute [latex]f(17)[/latex]. What does this quantity measure? Write a complete sentence to explain.
- If the model holds further into the future, when do we predict the ice cover will vanish?
- In light of your work above, what is a reasonable domain to use for the model[latex]A=f(t)[/latex]? What is the corresponding range?
Show Solution
a. To determine a linear model we need to find the slope and the vertical intercept. First, we determine the vertical intercept. The vertical intercept is when [latex]t = 0[/latex], which is [latex]1951[/latex]. So we have the point [latex](0,1951)[/latex] in the model. We also know that in the year 2007 the ice cover is 1555 [latex]\hspace{0.5mm} m^2[/latex], so the model includes the point [latex](7,1555)[/latex]. Now that we have two points on the model we can find the slope using the slope formula: [latex]m = \frac{1555-1951}{7-0} = -\frac{396}{7}[/latex]. So our model in slope intercept form is [latex]A = f(t) = -\frac{396}{7}t+1951[/latex].
b. The slope is [latex]-\frac{396}{7}[/latex], which means that every 7 years, the amount of ice cover on the mountain decreases by [latex]396 \hspace{0.5mm} m^2[/latex]. The A-intercept which is [latex]1951[/latex] is the initial amount of ice cover on Mt. Kilimanjaro in the year 2000.
c.
[latex]f(17) = \frac{-396}{7} \cdot 17 + 1951 = \frac{6925}{7} \approx 986.86[/latex].
In the year 2017, the amount of ice cover on Mt. Kilimanjaro is [latex]986.86 \hspace{0.5mm} m^2[/latex].
d. We want to predict when the ice cover will vanish which means there is zero ice cover on the mountain. So we will set our linear model from part a equal to [latex]0[/latex] and solve:
\begin{align*}
0 & = \frac{-396}{7}t+1951 \\
-1951 & = \frac{-396}{7} \\
\end{align*}
Now we multiply both sides by 7 to get:
\begin{align*}
-13657 & = -396t \\
t & \approx 34.49
\end{align*}
In about 35 years, the ice cover will vanish.
e. To determine a reasonable domain we first want to think about a reasonable range. The range represents the possible amount of ice on the mountain. It does not make sense to have a negative amount of ice cover. We also know that in the year 2000 the mountain starts with [latex]1951 \hspace{0.5mm} m^2 of ice[/latex]. So a reasonable range is [[latex]0,1951][/latex]. We then know it takes about 35 years for the ice to vanish and since it does not make sense to consider negative time a reasonable domain would be [latex][0,35][/latex].
Activity 1.4.4
In each of the following prompts, we investigate the linear functions in context.
- A town's population initially had [latex]28750[/latex] people present and then grows at a constant rate of [latex]825[/latex] people per year. Find a linear model [latex]P=f(t)[/latex] for the number of people in the town year [latex]t[/latex].
- A different town's population [latex]Q[/latex] is given by the function [latex]Q=g(t)=42505-465t[/latex]. What is the slope of this function and what is its meaning in the model? Write a complete sentence to explain.
- A spherical tank is being drained with a pump. Initially a tank is full with [latex]\frac{32\pi}{3}[/latex] cubic feet of water. Assume the tank is drained at a constant rate of [latex]1.2[/latex] cubic feet per minute. Find a linear model [latex]V=p(t)[/latex] for the total amount fo water in the tank at time [latex]t[/latex]. In addition, what is a reasonable domain for the model?
- A conical tank is being filled in such a way that the height of the water in the tank, [latex]h[/latex] (in feet), at time [latex]t[/latex] (in minutes) is given by the function [latex]h=q(t)=0.65t[/latex]. What can you say about how the water level is rising? Write at least one careful sentence to explain.
- Suppose we know that a 5-year old car's value is [latex]$10200[/latex], and that after [latex]10[/latex] years its value is [latex]$4600[/latex]. Find a linear function [latex]C=L(t)[/latex] whose output is the value of the car in year [latex]t[/latex]. What is a reasonable domain for the model? What is the value and meaning of the slope of the line? Write at least one careful sentence to explain.
Show Solution
a. [latex]P = f(t) = 825t+28750[/latex].
b. Slope [latex]= -465[/latex]. The slope meaning is that each year the population of the town decreases by [latex]465[/latex] people.
c. [latex]V(t) = P(t) = -1.2t+\frac{32\pi}{3}[/latex]. To determine a reasonable domain for the model we first need to find out how long it takes for to be empty. So, we set our equation[latex]V(t) = 0[/latex] and solve. So, [latex]0 = -1.2t+\frac{32\pi}{3}[/latex]. Doing some algebra gives [latex]t = \frac{32\pi}{3.6} \approx 27.92[/latex]. So domain is [latex][0,\frac{32\pi}{3.6}][/latex].
d. Interpretation of slope: The water is rising at [latex]0.65[/latex] meters per minute.
e. [latex]C = L(t) = -1120t+15800[/latex]. To determine a reasonable domain we first need to find out how long it takes for the car to be worth [latex]$0[/latex]. So, [latex]0=-1120t+15800[/latex]. Solving for t gives [latex]t = \frac{395}{25} \approx 14.107[/latex]. So the domain is [latex][0,\frac{395}{25}][/latex].
Interpretation of slope: each year, the value of the car depreciates by [latex]$1120[/latex].
